Wartości funkcji elementarnych, takich jak sin, cos, log, są obliczane za pomocą komputera w sposób przybliżony. Często stosuje się w tym celu wzory, które mają postać nieskończonych sum. Na przykład prawdziwy jest następujący wzór na wartość logarytmu naturalnego z liczby 2:
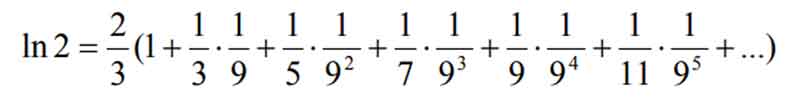
W oparciu o powyższy wzór można zaprojektować i napisać program, który dla danej liczby ε (ε > 0) oblicza przybliżoną wartość ln 2, sumując jak najmniej wyrazów, aby różnica między dwoma ostatnimi przybliżeniami była mniejsza niż ε.
Wprowadźmy oznaczenie:
dla n ≥ 1
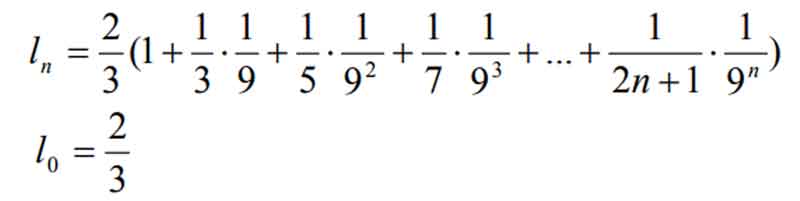
Wykonaj poniższe polecenia:
a) Wypełnij tabelę:
| n | ln |
| 0 | 2/3 |
| 1 | 2/3 * ( 1 + 1/3 * 1/9 ) |
| 2 | 2/3 * ( 1 + 1/3 * 1/9 + 1/5 * 1/92) |
| 3 | 2/3 * ( 1 + 1/3 * 1/9 + 1/5 * 1/92 + 1/7 *1/93 ) |
Poniżej podaj zależność pomiędzy wartościami ln i ln–1 dla każdego n=1, 2, …