Matura 2018 (maj). Zadanie 1. Analiza algorytmu
Rozważamy następujący algorytm:
Dane:
n – liczba całkowita dodatnia
Wynik:
p – liczba całkowita dodatnia
p ← 1 q ← n dopóki p < q wykonuj s ← (p+q) div 2 (*) jeżeli s*s*s < n wykonaj p ← s+1 w przeciwnym wypadku q ← s
Uwaga: zapis div oznacza dzielenie całkowite.
Zadanie 1.
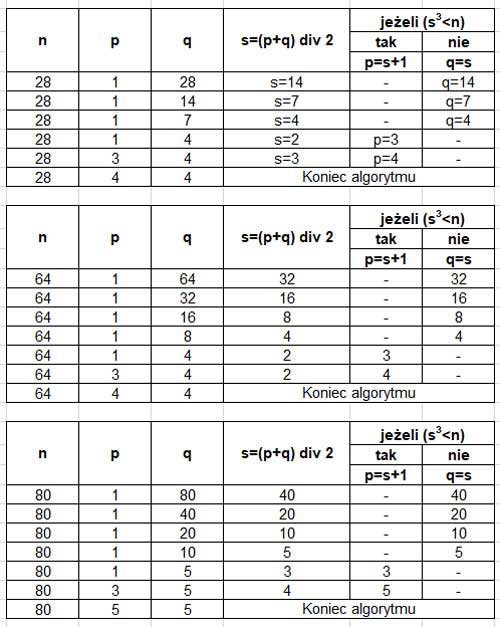
Podaj wynik działania algorytmu dla wskazanych w tabeli wartości n.
| n | p |
| 28 | 4 |
| 64 | 4 |
| 80 | 5 |
Miejsce na obliczenia.
Algorytm:
#include <iostream>
using namespace std;
int main()
{
cout << "Podaj n = ";
int n, p=1;
cin >> n;
int q=n;
int s;
while (p<q) {
s = (p+q)/2;
if (s*s*s<n)
p=s+1;
else
q=s;
}
cout << "p = " << p << endl;
return 0;
}
Zadanie 2.
Podaj najmniejszą oraz największą liczbę n, dla której wynikiem działania algorytmu będzie p = 10.
Miejsce na obliczenia.
Najmniejsza liczba n to 9*9*9+1=730, ponieważ musi być spełniony warunek s3<n. Największa liczba n to 10*10*10=1000, ponieważ musi być spełniony warunek s3<n.
Odpowiedź: Najmniejsza liczba to 730, największa liczba to 1000.
Zadanie 3.
Dokończ zdanie. Wybierz i zaznacz właściwą odpowiedź spośród podanych. Dla każdej liczby całkowitej n > 1 instrukcja oznaczona w algorytmie symbolem (*) wykona się
A. mniej niż 2*log2n razy.
B. więcej niż n/2, ale mniej niż n razy.
C. więcej niż n+1, ale mniej niż 2n razy.
D. więcej niż n2 razy.
Komentarz:
Odpowiedź A ponieważ, 2*log2n -> 2 * log264 = 2 * 6 = 12. Jest to mniej niż 12.
log264=x
2x = 64
26 = 64
kijank says:
Jak niby (5+1)div 2 to 2 a nie 3?
info says:
Dziękuje za znalezienie błędu, powinno być 3.