Matura 2018 (maj). Zadanie 2. Krajobraz
W pewnym paśmie górskim znajduje się n szczytów, które będziemy przedstawiać jako punkty w układzie kartezjańskim na płaszczyźnie. Wszystkie punkty leżą powyżej osi OX, tzn. druga współrzędna (y) każdego punktu jest dodatnia.
W punkcie (0,0) stoi obserwator. Jeśli dwa szczyty A i B mają współrzędne (xA, yA) oraz (xB, yB), to mówimy, że:
• szczyt A jest dla obserwatora widoczny na lewo od B, jeśli xA/yA < xB/yB;
• szczyt B jest widoczny na lewo od A, jeśli xA/yA > xB/yB.
Wiemy, że żadne dwa szczyty nie leżą w jednej linii z obserwatorem, a zatem dla obserwatora te szczyty nie zasłaniają się nawzajem. Ilustrację przykładowego położenia szczytów można zobaczyć na poniższym rysunku:
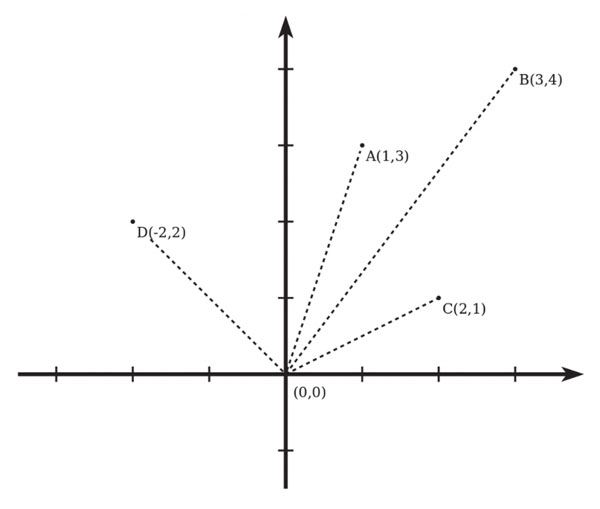
W tym przykładzie, patrząc od lewej do prawej strony, obserwator widzi kolejno szczyt D, szczyt A, szczyt B i szczyt C.
Współrzędne szczytów dane są w dwóch tablicach X[1..n] oraz Y[1..n] – szczyt numer i ma współrzędne (X[i], Y[i]).
Zadanie 1.
Napisz algorytm (w pseudokodzie lub wybranym języku programowania), który znajdzie i poda współrzędne skrajnie lewego szczytu, tzn. widocznego dla obserwatora na lewo od wszystkich pozostałych szczytów.
Specyfikacja:
Dane:
n – liczba całkowita dodatnia
X[1..n] – tablica liczb całkowitych
Y[1..n] – tablica liczb całkowitych dodatnich
Para (X[i], Y[i]) to współrzędne jednego szczytu, i = 1, 2, …, n.
Żadne dwa szczyty nie leżą w jednej linii z obserwatorem.
Wynik:
x, y – współrzędne skrajnie lewego szczytu spośród tych opisanych w tablicach X i Y.
Algorytm:
#include <iostream>
using namespace std;
int main()
{
int n=4;
int X[n]={1,3,2,-2};
int Y[n]={3,4,1,2};
int x,y;
for (int i=0; i<n-1; i++)
if (float(X[i])/float(Y[i]) < float(X[i+1])/float(Y[i+1])) {
x = X[i];
y = Y[i];
}
cout << x << " " << y << endl;
return 0;
}
Zadanie 2.
Napisz algorytm (w pseudokodzie lub wybranym języku programowania), który przestawi elementy tablic X i Y tak, aby szczyty były uporządkowane w kolejności, w której obserwator widzi je od lewej do prawej strony. Aby otrzymać maksymalną ocenę, Twój algorytm powinien mieć złożoność czasową kwadratową lub mniejszą. Algorytm może używać wyłącznie instrukcji sterujących, operatorów arytmetycznych, operatorów logicznych, porównań i przypisań do zmiennych. Zabronione jest używanie funkcji bibliotecznych dostępnych w językach programowania.
Specyfikacja:
Dane:
n – liczba całkowita dodatnia
X[1..n] – tablica liczb całkowitych
Y[1..n] – tablica liczb całkowitych dodatnich
Para (X[i], Y[i]) to współrzędne jednego szczytu, i = 1, 2, …, n.
Żadne dwa szczyty nie leżą w jednej linii z obserwatorem.
Wynik:
X[1..n], Y[1..n] – tablice zawierające współrzędne danych szczytów, uporządkowanych w kolejności, w której obserwator widzi je od lewej do prawej strony.
Algorytm:
#include <iostream>
using namespace std;
int main()
{
int n=4;
int X[n]={1,3,2,-2};
int Y[n]={3,4,1,2};
for (int j=0; j<n-1; j++)
for (int i=0; i<n-1; i++) {
if (float(X[i])/float(Y[i]) > float(X[i+1])/float(Y[i+1])) {
swap(X[i],X[i+1]);
swap(Y[i],Y[i+1]);
}
}
for (int i=0; i<n; i++) {
cout << "X[" << i << "]= " << X[i] << " ";
cout << "Y[" << i << "]= " << Y[i];
cout << endl;
}
return 0;
}
const int n says:
Błąd w 2 zadaniu.Zmienna n musi być konstantą.
info says:
Proszę o wyjaśnienie dlaczego zmienna n musi być stała?