Matura 2009 (maj). Zadanie 2. Ceny w systemach dziesiętnym i dwójkowym
W Dwójkolandii tradycyjnie ceny w sklepach są podawane w systemie dwójkowym. Ze względu na rosnący ruch turystów z innych krajów, gdzie wciąż obowiązuje system dziesiętny, rząd Dwójkolandii postanowił, że handlowcy mają obowiązek umieszczania cen w obu systemach.
- Pomóż właścicielowi baru szybkiej obsługi uzupełnić obowiązujący cennik:
| artykuł | cena w systemie dwójkowym | cena w systemie dziesiętnym |
| kakao | 111,11 | 7,75 |
| herbata czarna | 100,01 | 4,25 |
| herbata owocowa | 100,10 | 4,50 |
| capuccino | 101,00 | 5,00 |
| kawa espresso | 110,00 | 6,00 |
Wyjaśnienie:
- Rozdzielamy liczbę na część całkowitą i część ułamokową.
- Najpierw zajmiemy się częścią całkowitą, na przykładzie ceny:
kakao
111(2) = 1 * 20 + 1 * 21 + 1 * 22 = 1 + 2 + 4 = 7(10)
kawa espresso:
110(2) = 0 * 20 + 1 * 21 + 1 * 22 = 0 + 2 + 4 = 6(10)
Zamiana części całkowitej odbywa się za pomocą algorytmu:
Zamiana ceny w systemie binarnym na cenę w systemie dziesiętnym.
System dwójkowy jest najprostszym systemem pozycyjnym, w którym podstawa p = 2. System posiada dwie cyfry 0 i 1, zatem można je kodować bezpośrednio jednym bitem informacji. Wartość dziesiętna liczby zapisanej w naturalnym kodzie binarnym dana jest wzorem:
bn-1bn-2…b2b1b0 = bn-12n-1 + bn-22n-2 + … + b222 + b121 + b020
gdzie :
b – bit, cyfra dwójkowa 0 lub 1
n – liczba bitów w zapisie liczby
101011(2) = 25 + 23 + 21 + 20 = 32 + 8 + 2 + 1 = 43(10)
Zamiana ceny w systemie dziesiętnym na cenę w systemie binarnym.
W jednym kroku algorytmu wykonujemy czynności wyznaczenie reszty (%) z dzielenia przez dwa przekształcanej liczby oraz wykonujemy dzielenie całkowite przez dwa. Tę czynność wykonujemy tak długo, aż liczba dziesiętna będzie większa od 0 (zera).
- Kolejnym krokiem jest zamiana części ułamkowej, na przykładzie ceny:
kakao
0,11(2) = 1 * 2-1 + 1 * 2-2 = 1/2 + 1/4 = 0,5 + 0,25 = 0,75(10)
Zamiana ceny w systemie dziesiętnym na cenę w systemie binarnym w części ułamkowej.
Wykonujemy w taki sam sposób części całkowitej, z zapisem po przecinku.
Zamiana ceny w systemie binarnym na cenę w systemie dziesiętnym w części ułamkowej.
Obliczamy wartość części ułamkowej w następujący sposób:
0,111011(2) = 1 * 2-1 + 1 * 2-2 + 0 * 2-3 + 1 * 2-4 + 1 * 2-5 + 1 * 2-6 = 1/2 + 1/4 + 1/8 + 1/32 + 1/64 = 32/64 + 16/64 + 8/64 + 2/64 + 1/64 = 59/64
lub
0,111011(2) = 1 * 2-1 + 1 * 2-2 + 0 * 2-3 + 1 * 2-4 + 1 * 2-5 + 1 * 2-6 = 0,5 + 0,25 + 0,125 + 0,03125 + 0,015325 = 0,921875
Liczymy od pierwszej liczby po przecinku, mnożymy 1 lub 0 z 2 podniesioną do potęgi minusowej o odpowiedniej wartości, w zależności od pozycji danej liczby. pozycję liczymy od przecinka zaczynając od -1, -2, itd.
Liczbę należy zaokrąglić do dwóch miejsc po przecinku.
- Ostatnim krokiem jest połączenie dwóch części w całość (części całkowitej i ułamkowej).
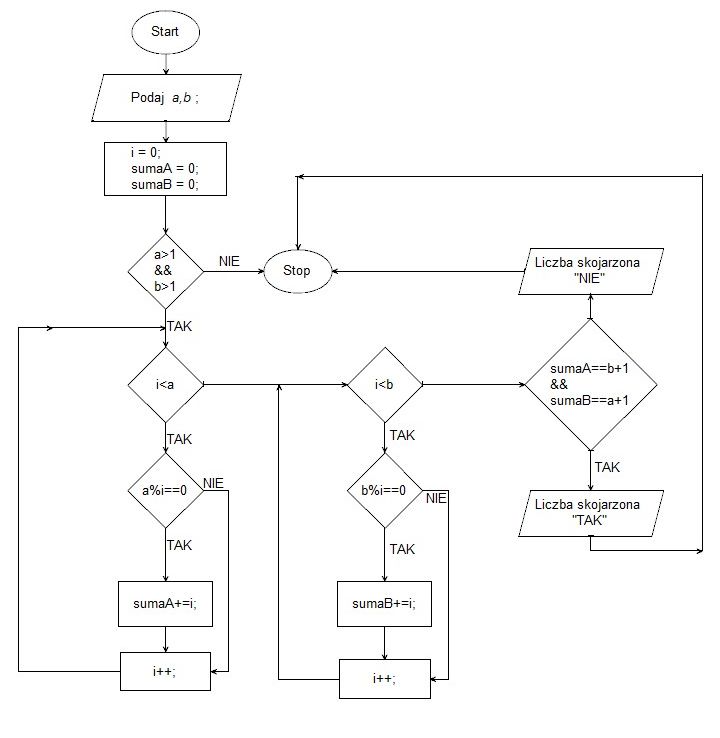
- Zaproponuj handlowcom metodę przeliczania cen z systemu dwójkowego na dziesiętny i zapisz ją w postaci algorytmu w wybranej przez siebie notacji (lista kroków, schemat blokowy lub język programowania, który wybrałeś/aś na egzamin). Uwzględnij, że ceny są podawane z dokładnością do dwóch miejsc po przecinku.
Specyfikacja:
Dane: s – napis złożony z ciągu zer i jedynek, przecinka oraz dwóch cyfr po przecinku (każda cyfra to 0 lub 1). Napis przed przecinkiem nie jest pusty.
Wynik: w – liczba oznaczająca wartość w systemie dziesiętnym liczby podanej w systemie dwójkowym w postaci napisu s.
#include <iostream>
#include <conio.h>
#include <math.h>
#include <iomanip>
using namespace std;
int main()
{
string cenaB, cenaB2="", cenaB3="";
int cenaD=0;
cout << "Podaj cene w systemie binarnym: ";
cin >> cenaB;
// pobieranie czesci calosci
int a=0;
while (cenaB[a] != ','){
cenaB2 += cenaB[a];
a++;
}
// pobieranie częsci ulamku
a++; // przesuniecie o przecinek
for (a;a<cenaB.length();a++) cenaB3 += cenaB[a];
// zamiana na dziesietna liczbe
int podstawa = 2;
int tmp = 1;
int x;
for (int i=cenaB2.length()-1; i>=0; i--) {
x = cenaB2[i]-48;
cenaD += x*tmp;
tmp *= podstawa;
}
// zamiana ulamku
double wynik=0, s=1;
for (int z=0; z<cenaB3.length(); z++){
if (cenaB3[z]=='1') {
wynik = wynik + pow(2,-s);
}
s++;
}
// wyswietlenie wyniku
cout << "Cena w systemie dziesietnym: ";
cout << fixed;
cout << setprecision(2);
cout << wynik+cenaD << endl;
return 0;
}