Matura 2016 (maj). Zadanie 4. Liczba PI
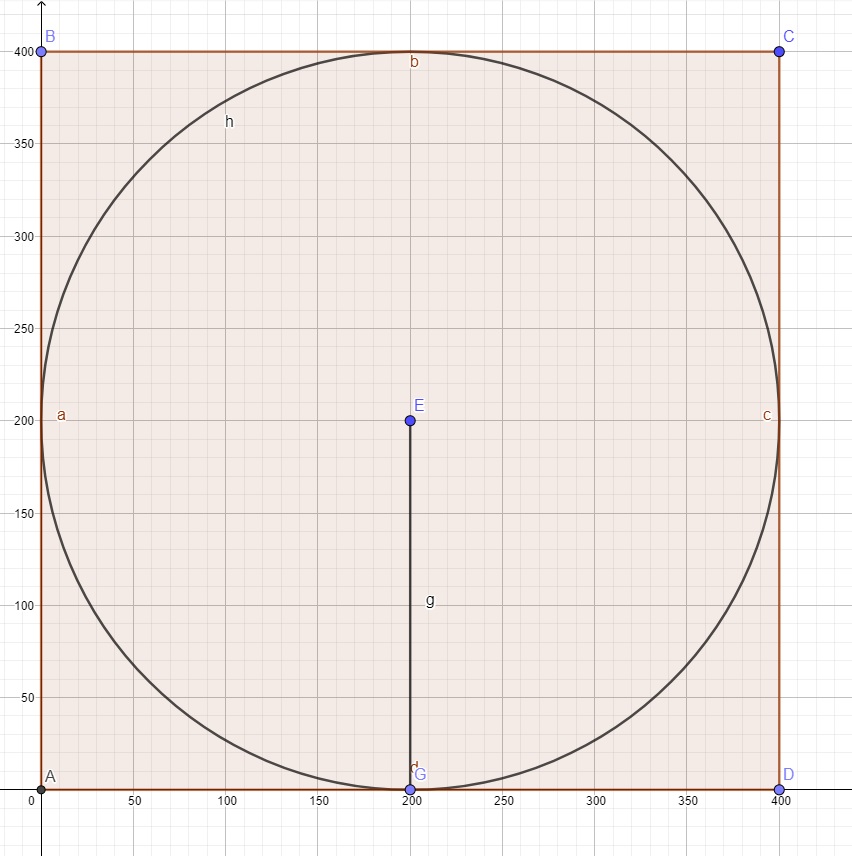
W kartezjańskim układzie współrzędnych na płaszczyźnie narysowano kwadrat o boku długości 400 i środku symetrii w punkcie (200;200). Boki kwadratu są równoległe do osi układu współrzędnych. W kwadrat wpisano koło. Następnie wylosowano 10 000 punktów należących do kwadratu. Współrzędne (x,y) punktów zostały zapisane w pliku punkty.txt, każdy punkt w osobnym wierszu. Wiersz ma postać dwóch liczb całkowitych z zakresu <0;400>, rozdzielonych pojedynczym znakiem odstępu.
Korzystając z powyższych danych oraz dostępnych narzędzi informatycznych, wykonaj zadania. Wyniki zapisz w pliku tekstowym wyniki_4.txt. Odpowiedź do każdego zadania poprzedź numerem tego zadania.
Zadanie 4.1. (0–3)
Wypisz współrzędne tych punktów, które należą do brzegu koła (okręgu), oraz podaj liczbę punktów należących do wnętrza koła (brzeg koła nie należy do wnętrza koła).
Wskazówka:
Równanie okręgu o środku w punkcie S = (a , b) i promieniu r > 0 ma postać:
( x – a ) 2 + ( y – b) 2= r 2
Informacja:
W pliku wśród 100 pierwszych punktów 80 należy do wnętrza koła.
Rozwiązanie:
Układ współrzędnych z wrysowanym kwadratem i kołem.
Plik .cpp rozwiązania zadania:
#include <iostream>
#include <fstream>
#define N 10000
using namespace std;
int main()
{
ifstream plik;
ofstream wyniki;
plik.open("punkty.txt");
wyniki.open("wyniki_4_1.txt");
// pobieranie danych do tablicy x i y
int x[N];
int y[N];
for (int i=0; i<N; i++)
plik >> x[i] >> y[i];
//srodek okregu S = ( a , b )
int a = 200, b = 200;
//promien okregu
int r = 200;
int ile = 0;
wyniki << "Wspolrzedne pkt nalezace do brzegu kola (okregu) : " << endl;
long wynik;
for (int i=0; i<N; i++) {
wynik = ((x[i]-a)*(x[i]-a))+((y[i]-b)*(y[i]-b));
//sprawdzam czy wspolrzedne naleza do brzegu kola
if (wynik == r*r){
wyniki << x[i] << " " << y[i] << endl;
}
//sprawdzam czy wspolrzedne naleza do wewnatrz kola
if (wynik < r*r)
ile++;
}
wyniki << "Ilosc pkt nalezacych do okregu: " << endl << ile << endl;
// zamkniecie plikow
plik.close();
wyniki.close();
return 0;
}
Zadanie 4.2. (0–3)
Przy założeniu równomiernego rozkładu punktów w kwadracie, stosunek liczby punktów nk należących do koła do liczby punktów n należących do kwadratu jest w przybliżeniu równy stosunkowi pola koła Pk do pola kwadratu P:
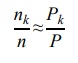
Dla przypomnienia:
P k = π * r 2
Wyznacz przybliżoną wartość liczby pi, biorąc pod uwagę punkty z pliku punkty.txt:
– pierwszych 1000 punktów,
– pierwszych 5000 punktów,
– wszystkie punkty.
Wyniki zaokrąglij do 4 miejsc po przecinku.
Informacja:
Przybliżona wartość liczby pi dla pierwszych 100 punktów z pliku wynosi 3,2000.
Rozwiązanie:
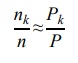
Ze stosunku podanego powyżej wynik, iż nk/n * 4 = pi.
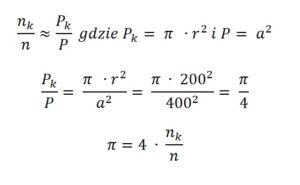
#include <iostream>
#include <fstream>
#include <iomanip>
#define N 10000
using namespace std;
int main()
{
ifstream plik;
ofstream wyniki;
plik.open("punkty.txt");
wyniki.open("wyniki_4.txt");
// pobieranie danych do tablicy x i y
int x[N];
int y[N];
for (int i=0; i<N; i++)
plik >> x[i] >> y[i];
//srodek okregu S = ( a , b )
int a = 200, b = 200;
//promien okregu
int r = 200;
int ile1000 = 0;
int ile5000 = 0;
int ile = 0;
long wynik;
for (int i=0; i<1000; i++) {
wynik = ((x[i]-a)*(x[i]-a))+((y[i]-b)*(y[i]-b));
if (wynik <= r*r) ile1000++;
}
for (int i=0; i<5000; i++) {
wynik = ((x[i]-a)*(x[i]-a))+((y[i]-b)*(y[i]-b));
if (wynik <= r*r) ile5000++;
}
for (int i=0; i<N; i++) {
wynik = ((x[i]-a)*(x[i]-a))+((y[i]-b)*(y[i]-b));
if (wynik <= r*r) ile++;
}
wyniki << "Ze wzoru wynika, iz stosunke Nk do N nalezy przemnozyc o 4." << endl;
wyniki << "Przyblizona wartosc liczby pi (pierwszych 1000 pkt): ";
wyniki << fixed;
//ustawia wyswietlana liczbe zmiennoprzecinkowa na notacje stala, potrzebna do tego biblioteka iomanip
wyniki << setprecision(4);
//ustawia dokladnosc wyswietlanej liczby na liczbe w nawiasie np. 4 to 0,0001
wyniki << (double(ile1000) / 1000) * 4 << endl;
wyniki << "Przyblizona wartosc liczby pi (pierwszych 5000 pkt): ";
wyniki << fixed;
wyniki << setprecision(4);
wyniki << (double(ile5000) / 5000) * 4 << endl;
wyniki << "Przyblizona wartosc liczby pi (wszystkich pkt): ";
wyniki << fixed;
wyniki << setprecision(4);
wyniki << (double(ile) / N) * 4 << endl;
// zamkniecie plikow
plik.close();
wyniki.close();
return 0;
}
Zadanie 4.3. (0−5)
Błąd bezwzględny przybliżonej wartości liczby pi, wyznaczonej z n punktów, definiujemy następująco:
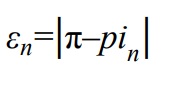
gdzie:
π – wartość liczby pi, będąca wynikiem standardowej funkcji z narzędzia informatycznego, z którego korzystasz;
pin – przybliżona wartość liczby pi wyznaczona z n kolejnych punktów, poczynając od pierwszego punktu z pliku punkty.txt, np. pi1000 – liczba wyznaczona z pierwszego tysiąca punktów.
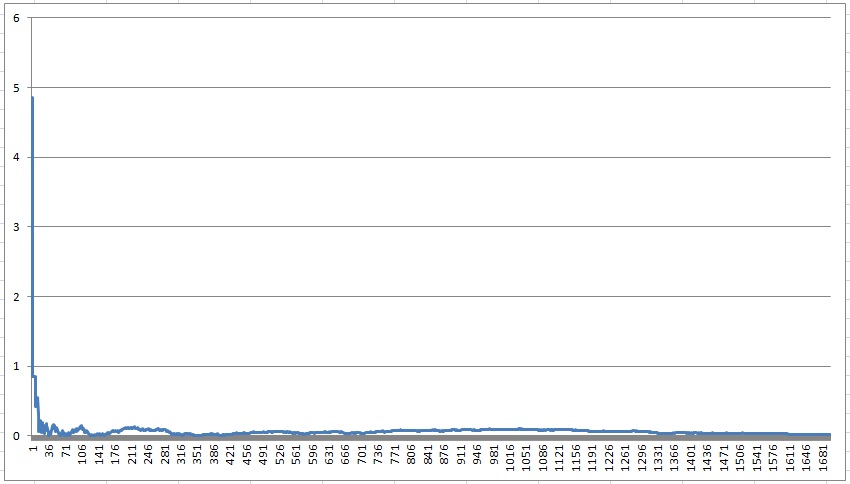
Oblicz εn dla n = 1, 2, 3, …, 1700. Na podstawie powyższego zestawienia utwórz wykres liniowy ilustrujący zmiany dokładności wyznaczanej liczby pi. Zadbaj o czytelność wykresu. Wartości dla ε1000 oraz ε1700 (zaokrąglone do czterech miejsc po przecinku) zapisz do pliku wyniki_4.txt.
Rozwiązanie:
#include <iostream>
#include <fstream>
#include <iomanip>
#include <cstdlib>
#include <math.h>
#define N 1700
using namespace std;
int main()
{
ifstream plik;
ofstream wyniki;
plik.open("punkty.txt");
wyniki.open("wyniki_4.txt");
// pobieranie danych do tablicy x i y
int x[N];
int y[N];
long n[N];
double w[N];
//srodek okregu S = ( a , b )
int a = 200, b = 200;
//promien okregu
int r = 200;
//ilosc punktow nalezacych do kola
int ile = 0;
//tmp wynik
long wynik;
for (int i=0; i<N; i++) {
plik >> x[i] >> y[i];
ile = 0;
for (int j=0; j<=i; j++) {
wynik = ((x[j]-a)*(x[j]-a))+((y[j]-b)*(y[j]-b));
if (wynik <=r*r) ile++;
}
n[i] = ile;
w[i] = fabs( M_PI - (double(ile) / i) * 4 ); // wartosc bezwzgledna liczby zmiennoprzecinkowej
}
for (int a=1; a<N; a++) {
wyniki << fixed;
wyniki << setprecision(4);
wyniki << w[a] << endl;
}
// zamkniecie plikow
plik.close();
wyniki.close();
return 0;
}
Część druga zadania (wykres):
- Pobieramy z pliku textowego dane do excela.
- Dane, które pobraliśmy są w formie tekstowej. Rozdzielone są kropką zamiast przecinkiem.
- Należy zamienić (CTR+H) kropkę (.) na przecinek (,).
- Zaznaczamy wszystkie dane pobrane z pliku txt i tworzymy wykres liniowy. Poprawiamy wygląd wykresu i gotowe!