Matura 2017 (maj). Zadania 2. Rekurencja

Matura 2017 (maj). Zadania 2. Rekurencja

Funkcja licz(x) przyjmuje jako argument dodatnią liczbę całkowitą x, natomiast jako wynik daje pewną liczbę całkowitą.

licz(x)
  jeżeli x = 1
     podaj wynik 1
   w przeciwnym przypadku
     w ← licz(x div 2)
     jeżeli x mod 2 = 1
       podaj wynik w+1
     w przeciwnym przypadku
       podaj wynik w-1

Uwaga: div – dzielenie całkowite, mod – reszta z dzielenia całkowitego.

Zadanie 1.

Uzupełnij tabelę – podaj wartość licz(x) dla podanych argumentów x.

x licz(x)
11 2
13 2
21 1
32 -4

Obliczenia:

Rekurencja działa na zasadzie wywoływania funkcji dopóki x nie będzie równy 1. Na zielono zaznaczyłem kod który wykona się przy x = 11.

licz(11) 
   jeżeli x = 1 
       podaj wynik 1 
   w przeciwnym przypadku 
      w ← licz(x div 2) // w = 11 div 2 = 5 
      jeżeli x mod 2 = 1 
         podaj wynik w+1 
      w przeciwnym przypadku 
         podaj wynik w-1

Zwróci nam wartość 5, ponieważ teraz w = 11 div 2 = 5. Teraz ponownie wywołujemy funkcje licz(x) z wartością x = 5.

licz(5) 
   jeżeli x = 1 
      podaj wynik 1 
   w przeciwnym przypadku 
      w ← licz(x div 2) // w = 5 div 2 = 2
      jeżeli x mod 2 = 1 
         podaj wynik w+1 
      w przeciwnym przypadku 
         podaj wynik w-1

Zwróci nam wartość 2, ponieważ teraz w = 5 div 2 = 2. Teraz ponownie wywołujemy funkcje licz(x) z wartością x = 2.

licz(2) 
   jeżeli x = 1 
      podaj wynik 1 
   w przeciwnym przypadku 
      w ← licz(x div 2) // w = 2 div 2 = 1
      jeżeli x mod 2 = 1 
         podaj wynik w+1 
      w przeciwnym przypadku 
         podaj wynik w-1

Zwróci nam wartość 1, ponieważ teraz w = 2 div 2 = 1. Teraz ponownie wywołujemy funkcje licz(x) z wartością x = 1, ale to już zwróci nam w = 1.

licz(1) 
   jeżeli x = 1 
      podaj wynik 1 
   w przeciwnym przypadku 
      w ← licz(x div 2) 
      jeżeli x mod 2 = 1 
         podaj wynik w+1 
      w przeciwnym przypadku 
         podaj wynik w-1

Musimy wrócić do naszych funkcji licz(x) i wykonać dalszą część kodu, którą zaznaczę kolorem czerwonym, wracamy do funkcji licz(2). Pamiętamy że w = 1.

licz(2) 
   jeżeli x = 1 
      podaj wynik 1 
   w przeciwnym przypadku 
      w ← licz(x div 2) // w = 2 div 2 = 1
      jeżeli x mod 2 = 1 // 2 mod 2 = 0
         podaj wynik w+1 
      w przeciwnym przypadku 
         podaj wynik w-1 // w = 1 – 1 = 0

Po wykonaniu tej funkcji w = 0, teraz wracamy do funkcji licz(5). 

licz(5) 
   jeżeli x = 1 
      podaj wynik 1 
   w przeciwnym przypadku 
      w ← licz(x div 2) // w = 5 div 2 = 2
      jeżeli x mod 2 = 1 // 5 mod 2 = 1 
         podaj wynik w+1 // w = 0 + 1 = 1 
      w przeciwnym przypadku 
         podaj wynik w-1

Po wykonaniu tej funkcji w = 1, teraz wracamy do funkcji licz(11).

licz(11) 
   jeżeli x = 1  
      podaj wynik 1 
   w przeciwnym przypadku 
      w ← licz(x div 2) // w = 11 div 2 = 5
      jeżeli x mod 2 = 1 // 11 mod 2 = 1 
         podaj wynik w+1 // w = 1 + 1 = 2 
      w przeciwnym przypadku 
         podaj wynik w-1

Po wykonaniu tej funkcji w = 2, teraz już nie mamy w pamięci żadnej funkcji licz(x), to wynik naszej funkcji zwraca wartość 2.

Pozostałe rozwiązania:

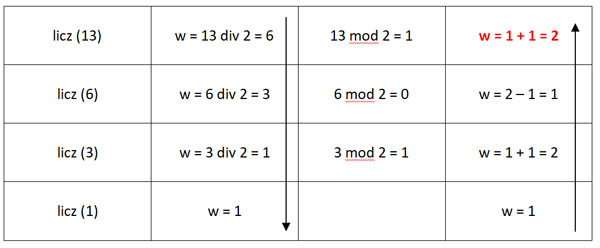
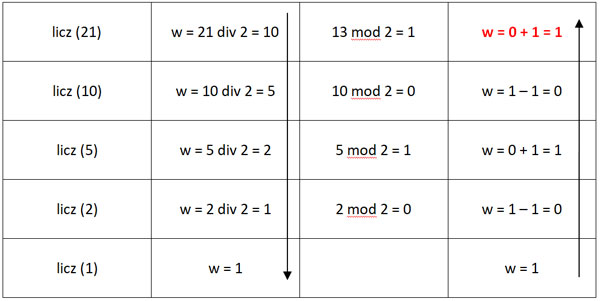
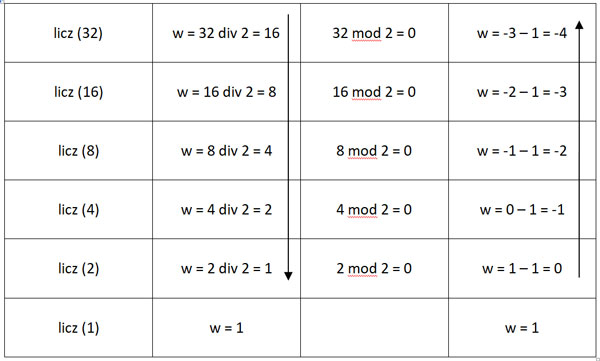
Zadanie 2.

Dana jest dodatnia liczba całkowita k. Jaka jest najmniejsza dodatnia liczba całkowita x, dla której obliczanie wartości licz(x) wymaga dokładnie k wywołań funkcji licz, licząc także pierwsze wywołanie licz(x)? Podkreśl prawidłową odpowiedź.

Przykład: obliczenie licz(13) wymaga dokładnie 4 wywołań funkcji licz.

A) x = k2
B) x = 2k–1
C) x = k+1
D) x = 2k

Przykład odpowiedzi nr 1:

Najmniejsza dodatnia liczba całkowita x, dla której dokładne będzie k wywołań funkcji licz() jest to liczba sprawdzając od początku jeden (1). Wywołanie funkcji licz(x) z wartością 1 wykona się dokładnie jeden raz, ponieważ: 

licz(1) 
   jeżeli x = 1 
      podaj wynik 1 
   w przeciwnym przypadku 
      w ← licz(x div 2) // w = 11 div 2 = 5
      jeżeli x mod 2 = 1 // 11 mod 2 = 1 
          podaj wynik w+1 // w = 1 + 1 = 2 
      w przeciwnym przypadku 
          podaj wynik w-1

W funkcji licz(1) wykona się tylko kod zaznaczony zielono i funkcja ta zwróci wynik 1. Następnie musimy sprawdzić dla jakiego k równe jest x, czyli kiedy x = k (1 = k).

Sprawdzamy dla x= 1: 

A)
x = k2
k = 1  ⇒ x = 12  ⇒ 1 = 1
B)
x = 2k–1 
k = 1  ⇒ x = 21-1  ⇒ x = 20  ⇒ 1 = 1 
C)
x = k+1
k = 0  ⇒ x = 0 + 1  ⇒ 1 = 1 (k musi być liczbą dodatnią całkowitą!!! To odpada!!!)
D) 
x = 2k
k = 0  ⇒ x = 20  ⇒ 1 = 1 (k musi być liczbą dodatnią całkowitą!!! To odpada!!!)

Mamy dwie odpowiedzi prawidłowe: A i B. Zastanawiając się, która odpowiedź jest prawidłowa i dlaczego jest to B, doszedłem do wniosku, iż musi to być to związane z liczbą binarną, dlatego postawiłem na odpowiedź B.

Przykład odpowiedzi nr 2 :

Jest to rozwiązanie, gdzie zostało założone, iż do sprawdzenia należy wybrać x ≠ 1. Padło na początek na liczbę x = 2 i tak dla tek liczby funkcja licz(2) wykona się dwa razy.

licz(2) ⇒ wywołań tej funkcji jest dokładnie 2 razy.

licz(2) ⇒ licz(1)

A)
x = k2
k = 2  ⇒ x = 22  ⇒ 2 = 4 ( to odpada ponieważ x = k2 )
B)
x = 2k–1 
k = 2  ⇒ x = 22-1  ⇒ x = 21  ⇒ 2 = 2  (ta odpowiedź jest prawidłowa)
C)
x = k+1
k = 2  ⇒ x = 2 + 1  ⇒ 2 = 3 (równanie to nie jest prawdziwe!!! To odpada!!!)
D) 
x = 2k
k = 2  ⇒ x = 22  ⇒ 2 = 4 (równanie to nie jest prawdziwe!!! To odpada!!!)

Odpowiedź jest prawidłowa, ale nie jest to najmniejsza dodatnia liczba całkowita. Tu moja uwaga, nie wiadomo co miał na myśli autor zadania.

Odpowiedź otrzymałem od Pana Jakuba. Dziękuje!!!

UWAGA!!! Jeśli ktoś ma bardziej racjonalne wyjaśnienie proszę napisać na kontakt@informatyka.dwojka.net. Dziękuję.

Zadanie 3.

Podaj najmniejszą liczbę całkowitą x większą od 100, dla której wynikiem wywołania licz(x) będzie 0.

Odpowiedź:

x = 135

Obliczenia:

W naszym przypadku podany algorytm jest to zamiana liczby dziesiętnej na liczbę binarną. W zadaniu tym należy wziąć po uwagę, kiedy otrzymamy wynik 0 (zero). Będzie to wtedy kiedy ilość zer i jedynej w liczbie binarnej będzie równa sobie. Kolejnym problem jest podanie liczy powyżej 10010, taka liczba zawiera 7 cyfr w zapisie binarnym. Szukamy liczby która w zapisie binarnym będzie miała parzystą ilość liczb, tj. w tym przypadku 8.

100000002 = 12810

Szukana najmniejsza liczba binarna zawierająca 8 cyfr, która składa się z 4 jedynek i 4 zer.

100001112 = 13510

Matura 2015 (maj). Zadanie 1. Problem telewidza

Matura 2015 (maj). Zadanie 1. Problem telewidza

W Problemie telewidza mamy program telewizyjny, zawierający listę filmów emitowanych w różnych stacjach telewizyjnych jednego dnia. Telewidz zamierza obejrzeć jak najwięcej filmów w całości. Jedyne ograniczenie jest takie, że telewidz może oglądać co najwyżej jeden film (stację telewizyjną) jednocześnie. Zakładamy, że jednego dnia wszystkie filmy są różne.

Program telewizyjny emisji filmów w 4 stacjach telewizyjnych:

Telewizja / stacja Film i godziny jego emisji Czas trwania emisji filmu
TV1 film 1: od 9:00 do 12:00
film 2: od 15:00 do 17:00		 3 godziny
2 godziny
TV2 film 3: od 11:00 do 16:00 5 godzin
TV3 film 4: od 12:00 do 14:00 2 godziny
TV4 film 5: od 11:30 do 12:30 1 godzina

Dla programu podanego powyżej telewidz jest w stanie obejrzeć aż trzy filmy, np.: film 1, film 4, film 2. Przyjmujemy, że telewidz nie traci w ogóle czasu na przełączanie pomiędzy stacjami (np. o godz. 12:00 z TV1 na TV3). Innymi słowy, czasy emisji filmów 1 i 4 nie kolidują ze sobą.
Rozważ następujący algorytm wyboru filmów do obejrzenia przez telewidza, w którym w kroku 2. stosuje się jedną z czterech strategii opisanych w tabeli 1.

Specyfikacja:

Dane:

T – zbiór filmów z programu telewizyjnego z godzinami emisji i czasami ich trwania,
S – strategia z tabeli 1.

Wynik:

P – zbiór filmów, które obejrzy telewidz.

Algorytm:

Krok 1. Zainicjuj P jako zbiór pusty.
Krok 2. Dopóki T zawiera jakieś filmy, wykonuj:
– stosując strategię S, wybierz ze zbioru T film x i usuń go z T
– dodaj film x do zbioru P
– usuń ze zbioru T wszystkie filmy, których czasy emisji kolidują z czasem emisji filmu x.
Krok 3. Zakończ wykonywanie algorytmu i wypisz wszystkie filmy ze zbioru P.

Tabela 1. Cztery strategie (S) w Problemie telewidza:

Strategia A Wybierz film, który trwa najdłużej, a jeśli jest takich więcej, to wybierz z nich ten, który się najwcześniej kończy. Jeśli jest więcej takich filmów,wybierz dowolny z nich.
Strategia B Wybierz film, który trwa najkrócej, a jeśli jest takich więcej, to wybierz z nich ten, który się najwcześniej kończy. Jeśli jest więcej takich filmów, wybierz dowolny z nich.
Strategia C Wybierz film, który się najwcześniej zaczyna, a jeśli jest takich więcej, to wybierz z nich ten, który się najwcześniej kończy. Jeśli jest więcej takich filmów, wybierz dowolny z nich.
Strategia D Wybierz film, który się najwcześniej kończy, a jeśli jest takich więcej, to wybierz z nich ten, który się najpóźniej zaczyna. Jeśli jest więcej takich filmów, wybierz dowolny z nich.

Przykład:
Dla podanego programu telewizyjnego zastosowanie w kroku 2. strategii A daje wynik P = {film 3}, czyli telewidz obejrzy tylko jeden film.

Zadanie 1.

Dla podanego programu telewizyjnego podaj wyniki wykonywania algorytmu po zastosowaniu strategii B, C i D:

Strategia S Zawartość zbioru P po zakończeniu wykonywania algorytmu
B P = {film 5, film 2}
C P = {film 1, film 4, film 2}
D P = {film 1, film 4, film 2}

Zadanie 2.

Zastosowana strategia S w algorytmie jest optymalna, jeśli dla każdego programu telewizyjnego wynik algorytmu (zbiór P) zawiera największą możliwą liczbę filmów, które może obejrzeć telewidz.

Uwaga:
Strategia A nie jest optymalna, ponieważ telewidz może obejrzeć trzy filmy: film 1, film 4 oraz film 2.

Dla strategii A, B i C podaj w przygotowanych tabelach przykłady programów telewizyjnych, z emisją czterech filmów w dwóch stacjach, będące dowodami, że żadna z tych strategii nie jest optymalna.

Dla każdej strategii i podanego dla niej programu telewizyjnego podaj wynik działania algorytmu oraz przykład ilustrujący, że telewidz może obejrzeć więcej filmów, jeżeli nie używa tej strategii.

Wskazówka. Podaj takie godziny emisji czterech filmów, aby telewidz był w stanie obejrzeć np. trzy lub więcej filmów, podczas gdy zastosowanie algorytmu z odpowiednią strategią daje rozwiązanie zawierające co najwyżej dwa filmy.

Dowód dla strategii A:

Telewizja / stacja Film i godziny jego emisji Czas trwania emisji filmu
TV1 film 1 (od …………………. do ………………….),
film 2 (od …………………. do ………………….)		 ………………….
………………….
TV2 film 3 (od …………………. do ………………….),
film 4 (od …………………. do ………………….)		 ………………….
………………….

Wynik działania algorytmu przy zastosowaniu strategii A:

P

Liczniejszy zbiór filmów, które może obejrzeć widz:

Z

Dowód dla strategii B:

Telewizja / stacja Film i godziny jego emisji Czas trwania emisji filmu
TV1 film 1 (od …………………. do ………………….),
film 2 (od …………………. do ………………….)		 ………………….
………………….
TV2 film 3 (od …………………. do ………………….),
film 4 (od …………………. do ………………….)		 ………………….
………………….

Wynik działania algorytmu przy zastosowaniu strategii B:

P

Liczniejszy zbiór filmów, które może obejrzeć widz:

Z

Dowód dla strategii C:

Telewizja / stacja Film i godziny jego emisji Czas trwania emisji filmu
TV1 film 1 (od …………………. do ………………….),
film 2 (od …………………. do ………………….)		 ………………….
………………….
TV2 film 3 (od …………………. do ………………….),
film 4 (od …………………. do ………………….)		 ………………….
………………….

Wynik działania algorytmu przy zastosowaniu strategii C:

P

Liczniejszy zbiór filmów, które może obejrzeć widz:

Z

 

Kurs PHP – Lekcja 02

Kurs PHP.
Składnia skryptu PHP.

 

Przypomnienie!!!
Poprzednio napisaliśmy swój pierwszy skrypt w php. Oto on:

<?php echo 'Witam na kursie PHP.'; ?>

Dowiedzieliśmy się również, że aby wykonywać polecenia języka PHP potrzebujesz zainstalowanego i uruchomione interpretera (czyli XAMPP’a).

UWAGA!!!
Aby wykonywać skrypt php musi on znajdować się w pliku z rozszerzeniem .php, NIE .html.

Składnia skryptu PHP.

Uruchom więc XAMPP’a i w folderze c:\xampp\www\KursPHP utwórz folder „lekcja02″. Następnie otwórz nowy plik w wybranym przez siebie edytorze i zapisz go w folderze lekcja02 jako plik index.php.

Możesz więc stworzyć sobie domyślną konstrukcję strony HTML czyli: <!DOCTYPE … <html><head> etc. ale aby wykonywać skrypty php na stronie musi mieć ona rozszerzenie .php.

Jak wygląda składnia zobaczyłeś w poprzedniej lekcji, ale dla przypomnienia, aby wykonać jakiekolwiek polecenie w języku PHP musi ono znajdować się pomiędzy znakiem rozpoczęcia i zamknięcia:

<!DOCTYPE html>
<html>
<head>
</head>
<body>
<!-- tutaj nie możesz wykonać skryptu php -->
<?php
  // tutaj zostanie wykonany skrypt php
?>
<!-- tutaj nie możesz wykonać skryptu php -->
<?php
  // tutaj znów możesz pisać w języku php
?>
</body>
</html>

Komentarze w PHP.

Komentarze w języku php możesz stosować na 3 sposoby.

1 sposób:

<?php   
// tutaj możesz dodać komentarz jedno linijny
?>

2 sposób:

<?php   
# tutaj możesz dodać komentarz jedno linijny
?>

3 sposób:

<?php   
/* 
tutaj możesz pisać wiele linii komentarza
kolejna linia i kolejna aż do zamknięcia komentarza
*/
?>

Integracja PHP z HTML.

Skrypty php możesz wykonywać w dowolnym miejscu całego dokumentu .php np. :

  • przed deklaracją doctype,
  • w sekcji head,
  • body,
  • nawet po znaczniku kończącym </html>
  • można powiedzieć w dowolnym miejscu dokumentu
  • możesz wstawiać również bardzo małe fragmenty kodu php wewnątrz znaczników html, przykład (zapisz plik w folderze c:\xampp\www\KursPHP\lekcja02 jako index.php):
<!DOCTYPE html>
<html>
<head>
</head>
<body>
<div id="<?php #dowolny skrypt ?>">
</div>
<a href="<?php echo 'http://google.com'; ?>">google</a>
</body>
</html>

Daje to naprawdę duże możliwości bo możesz na samym początku dokumentu wywołać skrypt, który zdecyduje czy strona ma się dalej ładować czy nie.

Co w efekcie jeśli sprawdzisz kod źródłowy uruchomionej strony będzie wyglądało następująco, możesz sprawdzić poprzez wyświetlenia źródła strony w przeglądarce internetowej:

<!DOCTYPE html> 
<html> 
<head> 
</head> 
<body> 
<div id=""> 
</div> 
<a href="http://google.com">google</a> 
</body> 
</html>

Uruchomienie skryptu możesz zobaczyć przechodząc do przeglądarki, wpisz localhost (musisz mieć włączonego XAMPP’a)
i kliknij poniżej Your Projects w KursPHP i w lekcja02.

UWAGA!!!
Zauważ również jedną bardzo ważną rzecz.
PHP to kod wykonywany po stronie serwera.
Czyli wszystko co wpiszesz pomiędzy znacznikami <?php ?> nie będzie widoczne w żaden sposób dla użytkowników.

Widoczne są tylko elementy, które poprzedzisz funkcją odpowiadającą za wyświetlanie tekstu. Taką bardzo popularną funkcją jest użyta wcześniej funkcja echo. Jeśli chcesz wyświetlić jakiś fragment tekstu przy pomocy php wywołujesz więc funkcję echo a następnie w cudzysłowie wpisujesz wybrany tekst. Działanie funkcji echo kończysz średnikiem – ; Budowa przypomina lekko css gdzie mamy cechę następnie wartość cechy i również kończymy ją średnikiem.

Matura 2016 (maj). Zadanie 4. Demografia

Matura 2016 (maj). Zadanie 4. Demografia

W pliku demografia.txt znajdują się informacje o urodzeniach, zgonach i ruchu naturalnym ludności w Polsce w roku 2009, w podziale na województwa i powiaty. Pierwszy wiersz w pliku jest wierszem nagłówkowym.

Fragment pliku demografia.txt:

powiat wojewodztwo ludnosc_ogolem wsp_urodzen wsp_zgonow saldo_migracji
augustowski podlaskie 58763 10,4 10,5 -1,1
bedzinski slaskie 150950 9,4 13 3,1
belchatowski lodzkie 112993 11,5 9,1 -1,6

Korzystając z dostępnych narzędzi informatycznych oraz danych zawartych w pliku demografia.txt, wykonaj podane polecenia. Odpowiedź do każdego zadania poprzedź numerem tego zadania.

Pobieranie danych do programu.

Zadanie 1.

Podaj liczbę powiatów należących do województwa mazowieckiego, w których saldo migracji było ujemne.

Rozwiązanie:

Komentarz:

Do obliczenia ilości powiatów z województwa mazowieckiego, których saldo migracji jest ujemne należy użyć filtra dla województwa – ustalamy mazowieckie, zaś dla kolumny saldo_migracji używamy filtra liczb -> mniejsza niż -> ustalamy wartość na 0 (zero). Ilość wyświetlonych wierszy jest równa 24.

Zadanie 2.

Współczynnik przyrostu naturalnego to różnica pomiędzy współczynnikiem urodzeń a współczynnikiem zgonów. Utwórz zestawienie 10 powiatów o największym współczynniku przyrostu naturalnego zawierające nazwę powiatu i współczynnik przyrostu naturalnego. Zestawienie uporządkuj alfabetycznie.

Rozwiązanie:

Komentarz:

Współczynnik przyrostu naturalnego obliczamy w nowej kolumnie G wykorzystując funkcję =D2-E2. Następnie sortujemy Z-A wg kolumny G. Następnie ukrywamy kolumny od B-F, a potem sortujemy wg powiatu tylko pierwszych dziesięć powiatów.

Zadanie 3.

Podaj nazwy czterech województw o największej liczbie ludności oraz liczbę ludności w tych województwach.

Rozwiązanie:

Komentarz:

W pierwszej kolejności należy wybrać wszystkie występujące województwa w naszym zestawieniu. Kolejnym krokiem jest obliczanie ilości mieszkańców dla każdego województwa, wykonujemy to za pomocą funkcji:

=SUMA.JEŻELI($B$2:$B$380;I2;$C$2:$C$380)

Zakres komórek z których sumujemy to wszystkie nazwy województw $B$2:$B$380, zaś suma to liczba mieszkańców w każdym powiecie należącym do województwa $C$2:$C$380. W funkcji tej występuję jeszcze I2, jest to nazwa województwa wpisana wcześniej. Sortujemy malejąco wg ilości sumy mieszkańców w danym województwie. Wybieramy pierwsze cztery rekordy.

Zadanie 4.

Współczynnik urodzeń to liczba urodzeń na 1000 mieszkańców, czyli:

Na podstawie podanej liczby ludności każdego powiatu (ludność ogółem) oraz współczynnika urodzeń w tym powiecie wykonaj dla województwa opolskiego zestawienie powiatów oraz liczby urodzeń w 2009 roku w każdym powiecie. Obliczoną liczbę urodzeń zaokrąglij w dół do najbliższej liczby całkowitej. Zestawienie posortuj alfabetycznie. Na podstawie powyższego zestawienia utwórz wykres kolumnowy ilustrujący liczbę urodzonych dzieci w poszczególnych powiatach. Pamiętaj o prawidłowym opisie wykresu.

Rozwiązanie:

Komentarz:

Rozwiązywanie zadania należy rozpocząć od wykonania sortowania wg województw, ponieważ musimy wykonać tylko dla województwa opolskiego. Następnie dla nowej kolumny tworzymy formułę odwrotną obliczającą liczbę urodzeń ze wzoru:

dzięki przekształceniu wzoru została utworzona formuła: =ZAOKR.DÓŁ(D180*C180/1000;0)

Na zakończenie tworzymy wykres z danych: nazwy powiatu województwa opolskiego i danych z kolumny G.

Plik z rozwiązaniem

Największy wspólny dzielnik

Największy wspólny dzielnik

Wyjaśnienie problemu

Największy wspólny dzielnik (NWD) dwóch liczb całkowitych – to największa liczba naturalna, która dzieli obie te liczby bez reszty.

Zatem metoda pierwsza

Największy wspólny dzielnik (NWD) znajduje się następująco. Rozkładem liczby na czynniki pierwsze, zakreślam wspólne dzielniki, mnożę zakreślone dzielniki i tak otrzymujemy liczbę będącą NWD.

Przykład

280 2 150 2
140 2 75 3
70 2 25 5
35 5 5 5
7 7 1
1

NWD(280,150) = 2 * 5 = 10

36 2 16 2
18 2 8 2
9 3 4 2
3 3 2 2
1 0 1

NWD(36,16) = 2 * 2 = 4

Zatem metoda druga

Algorytm Euklidesa jest szybkim sposobem obliczania największego wspólnego dzielnika dwóch (zwłaszcza dużych) liczb całkowitych. Polega ona na dzieleniu modulo (reszta z dzielenie).

Algorytm

Aby obliczyć NWD(a,b), wykonujemy kolejno następujące kroki:

  1. Dzielimy z resztą liczbę a przez liczbę b
    • jeżeli reszta =0, to NWD(a,b)=b
    • jeżeli reszta ?0, to przypisujemy liczbie a wartość liczby b, liczbie b wartość otrzymanej reszty, a następnie wykonujemy ponownie punkt 1.

Przykład

Liczba A = 280  B = 150

280 : 150 = 1 reszty 130
150 : 130 = 1 reszty 20
130 : 20 = 6 reszty 10
20 : 10 = 2 reszty 0

Otrzymaliśmy resztę równą zero, zatem szukany NWD będzie równy ostatniej niezerowej reszcie:

NWD(280, 150) = 10

Zatem metoda trzecia

Największy wspólny dzielnik (NWD) możemy wyznaczyć metodą Euklidesa, która polega na wyznaczeniu dwóch liczb naturalnych. Kolejnym krokiem jest sprawdzenie, która liczba jest większa i zamianie miejscami jeśli to konieczne, aby ustawić większa liczba na początku. Następnie wykonujemy odejmowanie, powstały wynik podstawiamy pod liczbę większą, gdzie powstaje nowa para. Powtarzamy te czynności do momentu, kiedy dwie liczby są równe.

Przykład

Liczba A = 280 B = 150

280 – 150 = 130
150 – 130= 20
130 – 20 = 110
110 – 20 = 90
90 – 20 = 70
70 – 20 = 50
50 -20 = 30
30 – 20 = 10
20 – 10 = 10
10 10

Ponieważ liczby są sobie równe, oznacza to, że największy wspólny dzielnik liczb 280 i 150 to 10.