Matura 2014. Zadanie 4. Działki

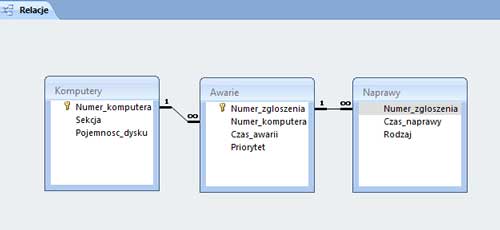
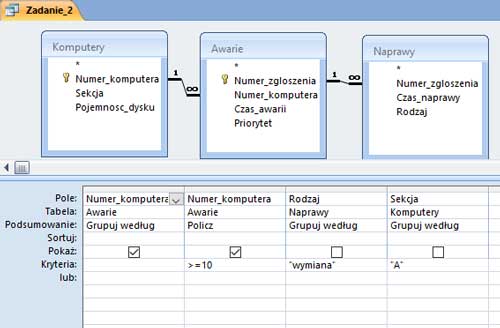
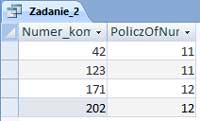
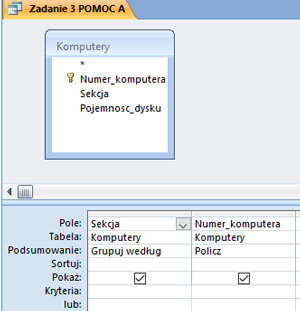
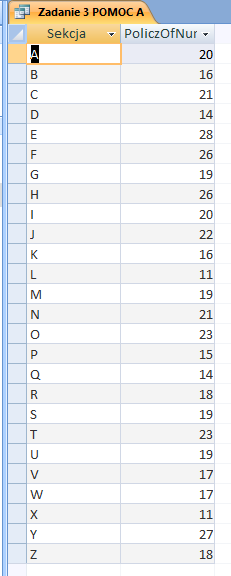
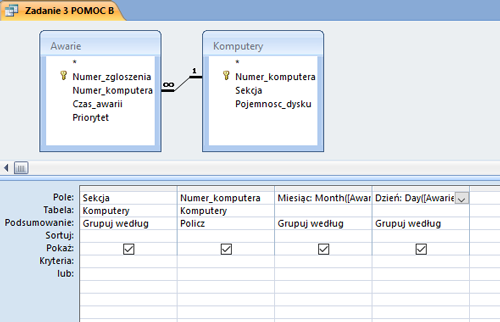
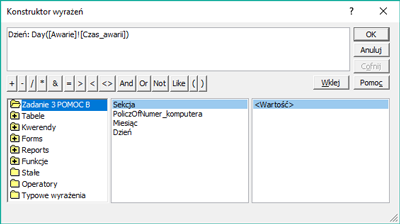
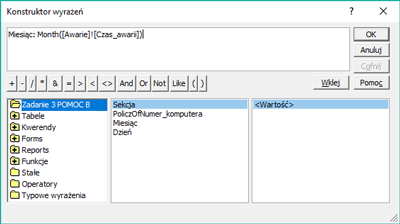
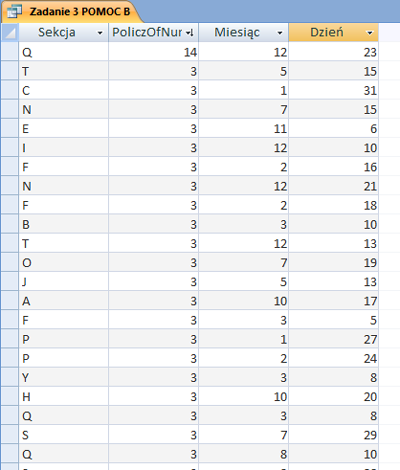
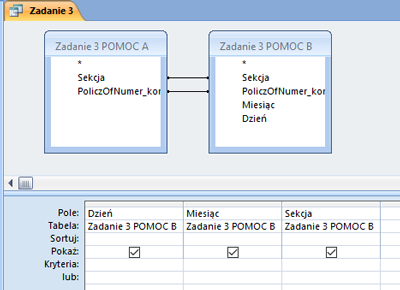
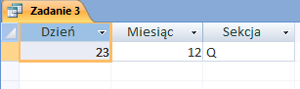
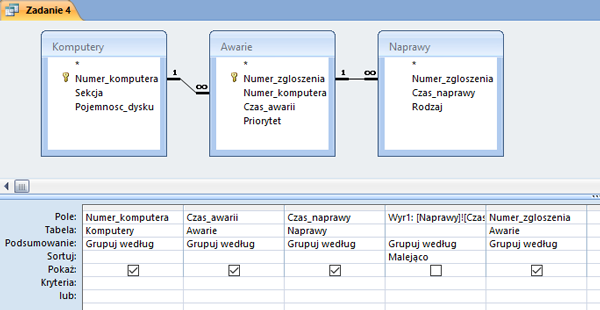
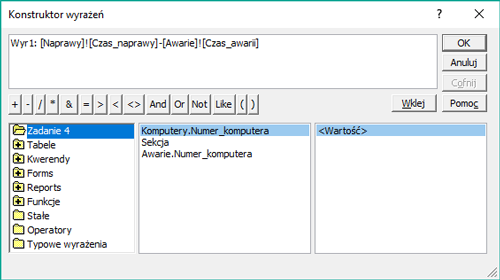
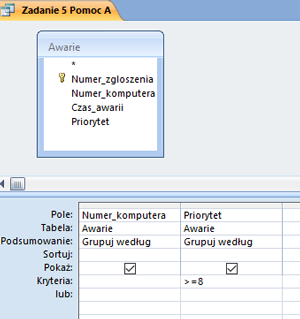
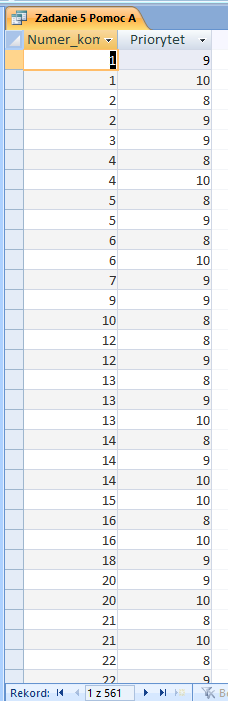
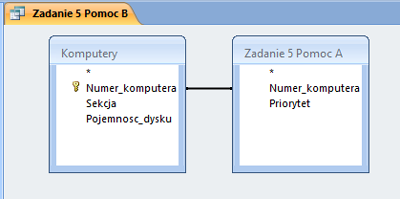
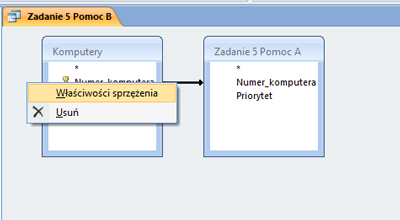
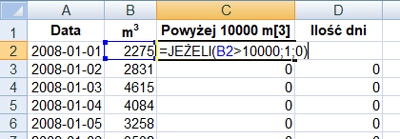
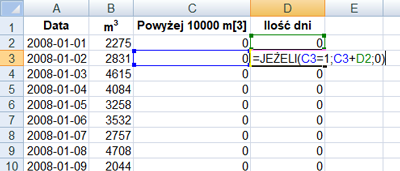
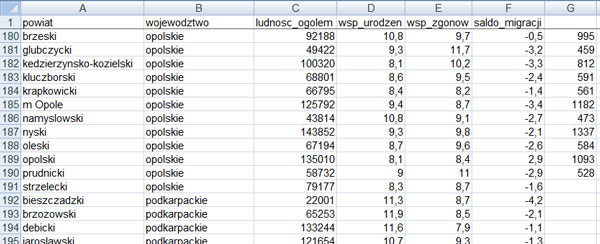
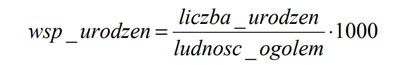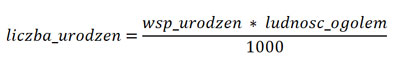W pliku DZIALKI.TXT znajduje się 5000 wierszy z informacjami o działkach w gminie Bajtocja, poprzedzonych wierszem nagłówkowym. W każdym wierszu znajdują się dane jednej działki, rozdzielone średnikami: numer (Numer), powierzchnia w metrach kwadratowych (Powierzchnia), oznaczenie rodzaju działki (Rodzaj), typ ulgi (Ulga).

Przykład:
Numer;Powierzchnia;Rodzaj;Ulga
517/10;1293,99;B;B
517/11;971,09;B;A
517/12;1259,19;R;B

Właściciele działek płacą gminie podatek. Podatek od działki jest obliczany jako iloczyn powierzchni działki i następującej stawki za metr kwadratowy [m2]:

rodzaj działki oznaczenie stawka za m2
rolna R 0,65 zł
budowlana B 0,77 zł
siedliskowa S 0,21 zł
leśna L 0,04 zł
rekreacyjna X 0,43 zł

Obliczona kwota podatku powinna jest zaokrąglana do dwóch miejsc po przecinku.

W gminie obowiązują cztery kategorie ulg. Kwota podatku pomniejszona jest o wielkość ulgi według następujących stawek:

oznaczenie ulgi ulga w procentach
A 20%
B 50%
C 90%
D 0%

Kwota podatku po uwzględnieniu ulgi również jest zaokrąglana do dwóch miejsc po przecinku.

Przykład:

Dla następującego wiersza danych: 517/12;1259,19;R;B, pełny podatek wynosi 1259,19 * 0,65 zł = 818,47 zł, a po uwzględnieniu ulgi jest on równy 409,24 zł i taka kwota jest wpłacana do kasy gminy.

Wykorzystując dane zawarte w pliku DZIALKI.TXT i dostępne narzędzia informatyczne, wykonaj podane polecenia. Odpowiedzi do poszczególnych podpunktów zapisz w kolejnych wierszach pliku tekstowego ZADANIE4.TXT. Odpowiedź do każdego podpunktu poprzedź literą oznaczającą ten podpunkt.

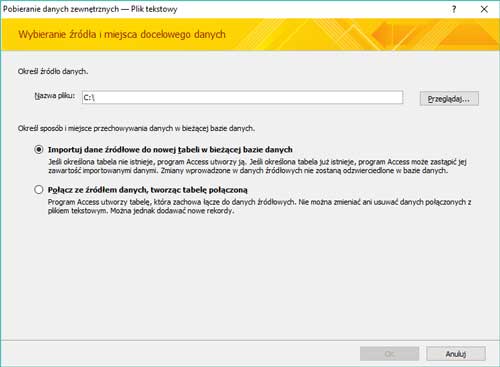
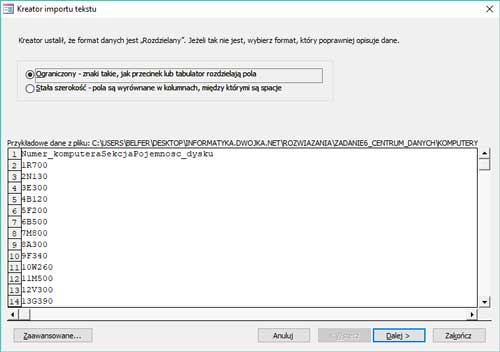
  1. Dodawanie danych do programu Excel.

2. Wybór pliku z danymi (DZIALKI.TXT).

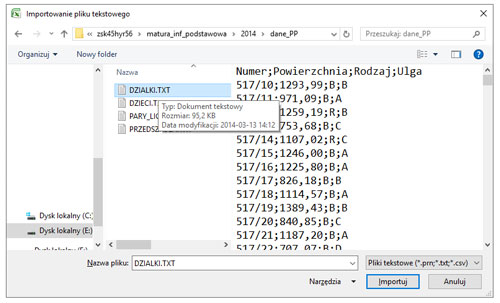
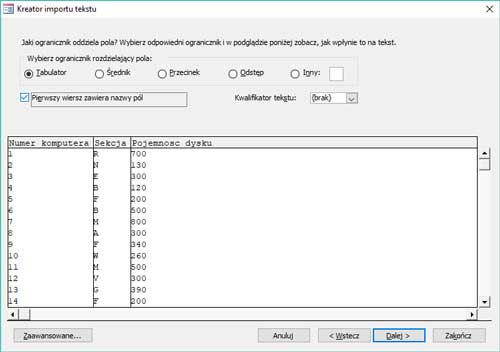
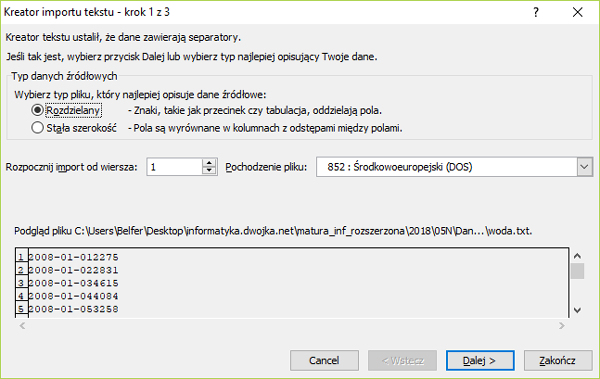
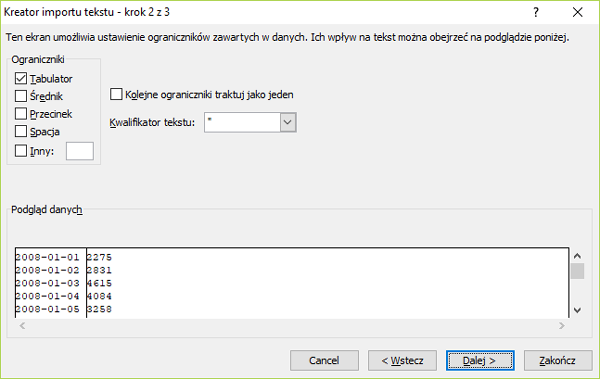
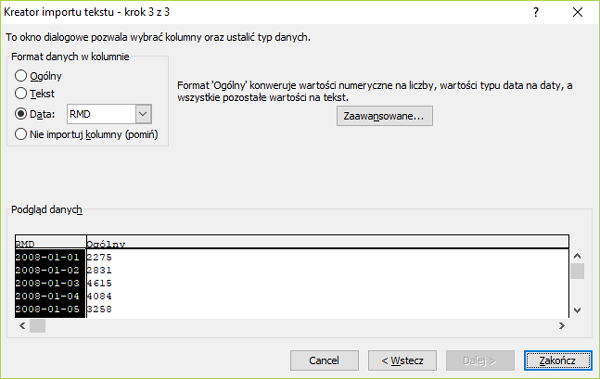
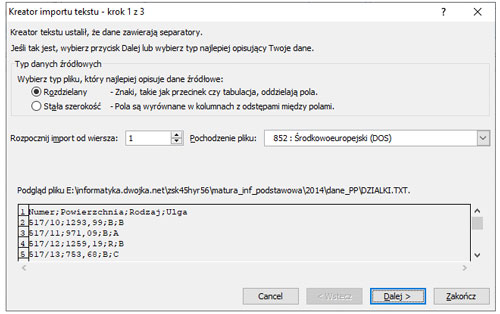
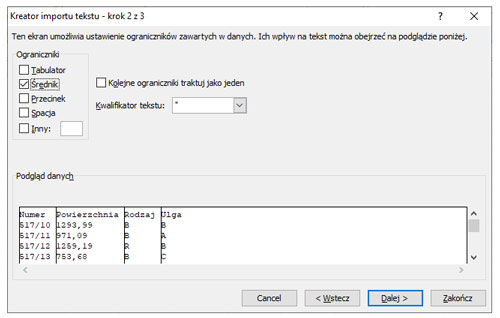
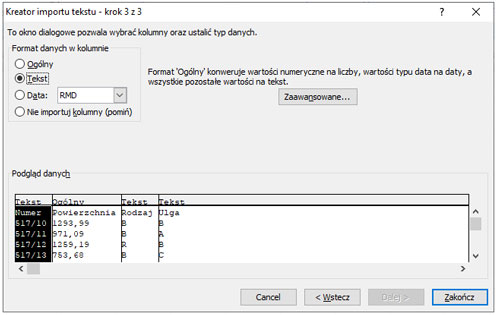
3. Za pomocą kreatora dodajemy dane rozdzielone średnikiem.

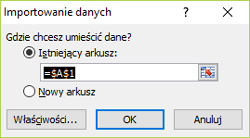
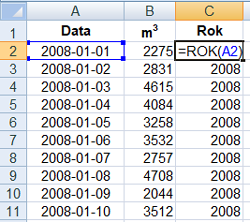
4. Wskazujemy miejsce importowania danych.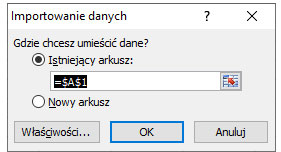

a) Podaj powierzchnię i rodzaj najmniejszej działki oraz powierzchnię i rodzaj największej działki.

Rozwiązanie:

Należy wykonać dwie czynności, po pierwsze należy znaleźć najmniejszą i największą powierzchnię działki wykorzystując odpowiednio funkcję:

= MIN(B2:B5001)

= MAX(B2:B5001)

Jak zostały znalezione powierzchnie najmniejsza i największa, musimy sprawdzić jaki jest rodzaj działki wykorzystując funkcję:

=WYSZUKAJ.PIONOWO(G9;B1:C5001;2;FAŁSZ)

Opis tej funkcji znajdziemy na stronie: MICROSOFT OFFICE

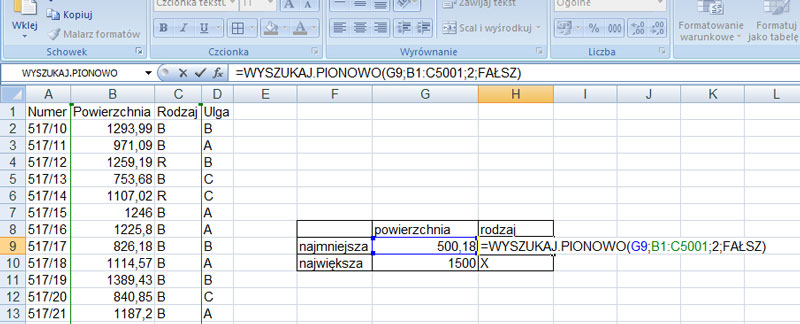
Rozwiązanie zadania:

powierzchnia rodzaj
najmniejsza 500,18 S
największa 1500 X

b) Utwórz zestawienie zawierające, dla każdego z rodzajów działek, następujące informacje: rodzaj działki, liczbę działek tego rodzaju, średnią powierzchnię (zaokrągloną do dwóch miejsc po przecinku) działek tego rodzaju.

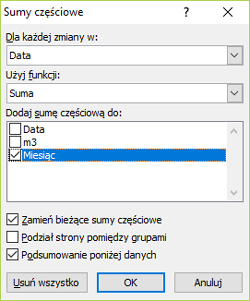
Do rozwiązania tego zadania będziemy musieli posortować dane wg rodzaju działki.

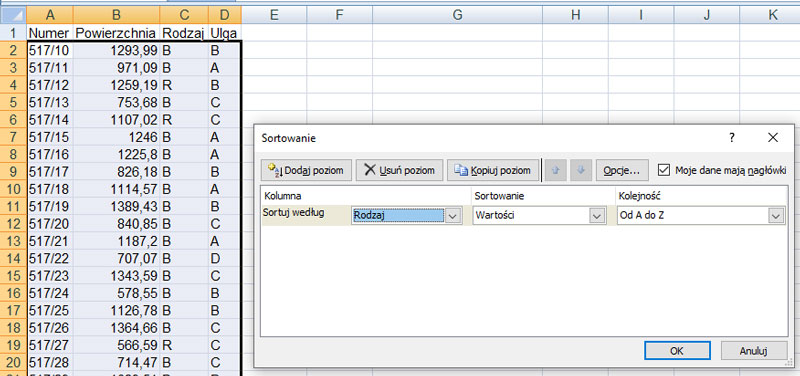
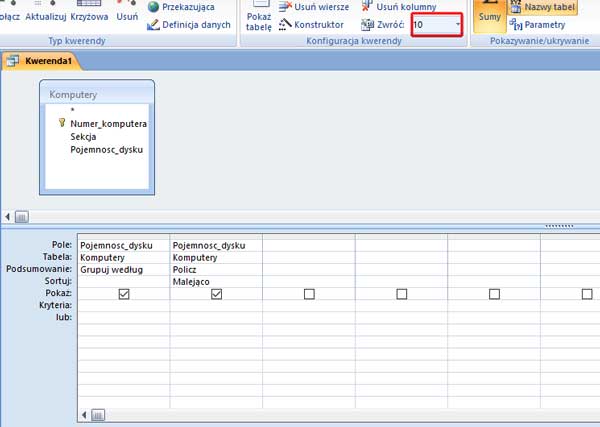
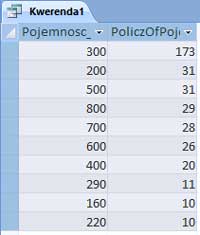
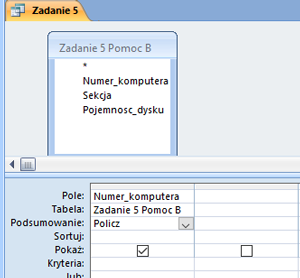
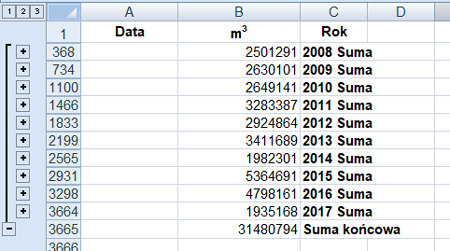
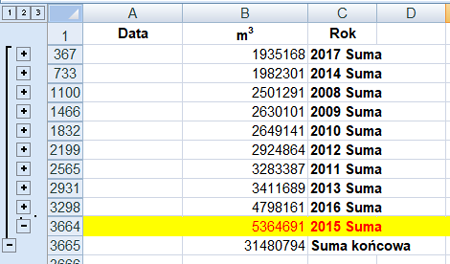
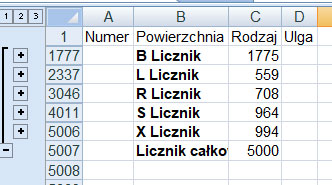
Następnie wykorzystam sumy częściowe do zebrania wszystkich danych, pierwsze dane to liczba poszczególnych działek:

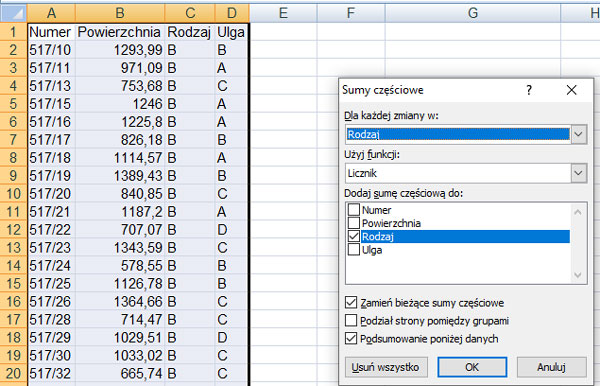
Drugie dane to średnia powierzchnia każdego rodzaju:

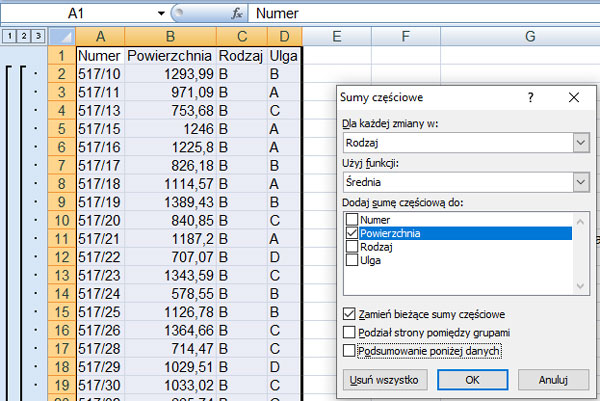
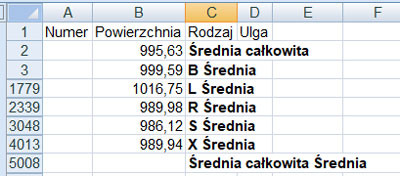
Rodzaj działki B L R S X
Liczba działek tego rodzaju 1775 559 708 964 994
Średnia powierzchnia 999,59 1016,75 989,98 986,12 989,94

 

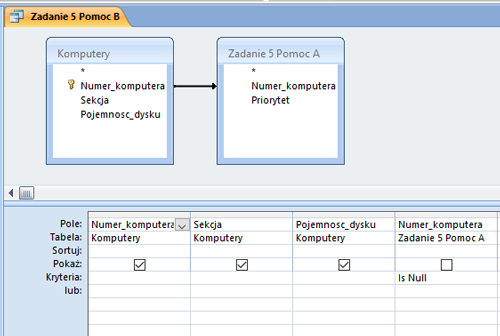
c) Utwórz zestawienie, w którym podasz ile jest działek, od których trzeba zapłacić podatek (według stawek i ulg wyszczególnionych w tabelach) w podanych poniżej tabeli przedziałach:

 

Wielkość podatku Liczba działek
do 100 zł włącznie
ponad 100 zł, ale do 500 zł włącznie
ponad 500 zł

Sporządź wykres procentowy ilustrujący otrzymane zestawienie. Pamiętaj o prawidłowym i czytelnym opisie wykresu.

Matura 2017 (maj). Zadania 2. Rekurencja

Matura 2017 (maj). Zadania 2. Rekurencja

Funkcja licz(x) przyjmuje jako argument dodatnią liczbę całkowitą x, natomiast jako wynik daje pewną liczbę całkowitą.

licz(x)
  jeżeli x = 1
     podaj wynik 1
   w przeciwnym przypadku
     w ← licz(x div 2)
     jeżeli x mod 2 = 1
       podaj wynik w+1
     w przeciwnym przypadku
       podaj wynik w-1

Uwaga: div – dzielenie całkowite, mod – reszta z dzielenia całkowitego.

Zadanie 1.

Uzupełnij tabelę – podaj wartość licz(x) dla podanych argumentów x.

x licz(x)
11 2
13 2
21 1
32 -4

Obliczenia:

Rekurencja działa na zasadzie wywoływania funkcji dopóki x nie będzie równy 1. Na zielono zaznaczyłem kod który wykona się przy x = 11.

licz(11) 
   jeżeli x = 1 
       podaj wynik 1 
   w przeciwnym przypadku 
      w ← licz(x div 2) // w = 11 div 2 = 5 
      jeżeli x mod 2 = 1 
         podaj wynik w+1 
      w przeciwnym przypadku 
         podaj wynik w-1

Zwróci nam wartość 5, ponieważ teraz w = 11 div 2 = 5. Teraz ponownie wywołujemy funkcje licz(x) z wartością x = 5.

licz(5) 
   jeżeli x = 1 
      podaj wynik 1 
   w przeciwnym przypadku 
      w ← licz(x div 2) // w = 5 div 2 = 2
      jeżeli x mod 2 = 1 
         podaj wynik w+1 
      w przeciwnym przypadku 
         podaj wynik w-1

Zwróci nam wartość 2, ponieważ teraz w = 5 div 2 = 2. Teraz ponownie wywołujemy funkcje licz(x) z wartością x = 2.

licz(2) 
   jeżeli x = 1 
      podaj wynik 1 
   w przeciwnym przypadku 
      w ← licz(x div 2) // w = 2 div 2 = 1
      jeżeli x mod 2 = 1 
         podaj wynik w+1 
      w przeciwnym przypadku 
         podaj wynik w-1

Zwróci nam wartość 1, ponieważ teraz w = 2 div 2 = 1. Teraz ponownie wywołujemy funkcje licz(x) z wartością x = 1, ale to już zwróci nam w = 1.

licz(1) 
   jeżeli x = 1 
      podaj wynik 1 
   w przeciwnym przypadku 
      w ← licz(x div 2) 
      jeżeli x mod 2 = 1 
         podaj wynik w+1 
      w przeciwnym przypadku 
         podaj wynik w-1

Musimy wrócić do naszych funkcji licz(x) i wykonać dalszą część kodu, którą zaznaczę kolorem czerwonym, wracamy do funkcji licz(2). Pamiętamy że w = 1.

licz(2) 
   jeżeli x = 1 
      podaj wynik 1 
   w przeciwnym przypadku 
      w ← licz(x div 2) // w = 2 div 2 = 1
      jeżeli x mod 2 = 1 // 2 mod 2 = 0
         podaj wynik w+1 
      w przeciwnym przypadku 
         podaj wynik w-1 // w = 1 – 1 = 0

Po wykonaniu tej funkcji w = 0, teraz wracamy do funkcji licz(5). 

licz(5) 
   jeżeli x = 1 
      podaj wynik 1 
   w przeciwnym przypadku 
      w ← licz(x div 2) // w = 5 div 2 = 2
      jeżeli x mod 2 = 1 // 5 mod 2 = 1 
         podaj wynik w+1 // w = 0 + 1 = 1 
      w przeciwnym przypadku 
         podaj wynik w-1

Po wykonaniu tej funkcji w = 1, teraz wracamy do funkcji licz(11).

licz(11) 
   jeżeli x = 1  
      podaj wynik 1 
   w przeciwnym przypadku 
      w ← licz(x div 2) // w = 11 div 2 = 5
      jeżeli x mod 2 = 1 // 11 mod 2 = 1 
         podaj wynik w+1 // w = 1 + 1 = 2 
      w przeciwnym przypadku 
         podaj wynik w-1

Po wykonaniu tej funkcji w = 2, teraz już nie mamy w pamięci żadnej funkcji licz(x), to wynik naszej funkcji zwraca wartość 2.

Pozostałe rozwiązania:

Zadanie 2.

Dana jest dodatnia liczba całkowita k. Jaka jest najmniejsza dodatnia liczba całkowita x, dla której obliczanie wartości licz(x) wymaga dokładnie k wywołań funkcji licz, licząc także pierwsze wywołanie licz(x)? Podkreśl prawidłową odpowiedź.

Przykład: obliczenie licz(13) wymaga dokładnie 4 wywołań funkcji licz.

A) x = k2
B) x = 2k–1
C) x = k+1
D) x = 2k

Przykład odpowiedzi nr 1:

Najmniejsza dodatnia liczba całkowita x, dla której dokładne będzie k wywołań funkcji licz() jest to liczba sprawdzając od początku jeden (1). Wywołanie funkcji licz(x) z wartością 1 wykona się dokładnie jeden raz, ponieważ: 

licz(1) 
   jeżeli x = 1 
      podaj wynik 1 
   w przeciwnym przypadku 
      w ← licz(x div 2) // w = 11 div 2 = 5
      jeżeli x mod 2 = 1 // 11 mod 2 = 1 
          podaj wynik w+1 // w = 1 + 1 = 2 
      w przeciwnym przypadku 
          podaj wynik w-1

W funkcji licz(1) wykona się tylko kod zaznaczony zielono i funkcja ta zwróci wynik 1. Następnie musimy sprawdzić dla jakiego k równe jest x, czyli kiedy x = k (1 = k).

Sprawdzamy dla x= 1: 

A)
x = k2
k = 1  ⇒ x = 12  ⇒ 1 = 1
B)
x = 2k–1 
k = 1  ⇒ x = 21-1  ⇒ x = 20  ⇒ 1 = 1 
C)
x = k+1
k = 0  ⇒ x = 0 + 1  ⇒ 1 = 1 (k musi być liczbą dodatnią całkowitą!!! To odpada!!!)
D) 
x = 2k
k = 0  ⇒ x = 20  ⇒ 1 = 1 (k musi być liczbą dodatnią całkowitą!!! To odpada!!!)

Mamy dwie odpowiedzi prawidłowe: A i B. Zastanawiając się, która odpowiedź jest prawidłowa i dlaczego jest to B, doszedłem do wniosku, iż musi to być to związane z liczbą binarną, dlatego postawiłem na odpowiedź B.

Przykład odpowiedzi nr 2 :

Jest to rozwiązanie, gdzie zostało założone, iż do sprawdzenia należy wybrać x ≠ 1. Padło na początek na liczbę x = 2 i tak dla tek liczby funkcja licz(2) wykona się dwa razy.

licz(2) ⇒ wywołań tej funkcji jest dokładnie 2 razy.

licz(2) ⇒ licz(1)

A)
x = k2
k = 2  ⇒ x = 22  ⇒ 2 = 4 ( to odpada ponieważ x = k2 )
B)
x = 2k–1 
k = 2  ⇒ x = 22-1  ⇒ x = 21  ⇒ 2 = 2  (ta odpowiedź jest prawidłowa)
C)
x = k+1
k = 2  ⇒ x = 2 + 1  ⇒ 2 = 3 (równanie to nie jest prawdziwe!!! To odpada!!!)
D) 
x = 2k
k = 2  ⇒ x = 22  ⇒ 2 = 4 (równanie to nie jest prawdziwe!!! To odpada!!!)

Odpowiedź jest prawidłowa, ale nie jest to najmniejsza dodatnia liczba całkowita. Tu moja uwaga, nie wiadomo co miał na myśli autor zadania.

Odpowiedź otrzymałem od Pana Jakuba. Dziękuje!!!

UWAGA!!! Jeśli ktoś ma bardziej racjonalne wyjaśnienie proszę napisać na kontakt@informatyka.dwojka.net. Dziękuję.

Zadanie 3.

Podaj najmniejszą liczbę całkowitą x większą od 100, dla której wynikiem wywołania licz(x) będzie 0.

Odpowiedź:

x = 135

Obliczenia:

W naszym przypadku podany algorytm jest to zamiana liczby dziesiętnej na liczbę binarną. W zadaniu tym należy wziąć po uwagę, kiedy otrzymamy wynik 0 (zero). Będzie to wtedy kiedy ilość zer i jedynej w liczbie binarnej będzie równa sobie. Kolejnym problem jest podanie liczy powyżej 10010, taka liczba zawiera 7 cyfr w zapisie binarnym. Szukamy liczby która w zapisie binarnym będzie miała parzystą ilość liczb, tj. w tym przypadku 8.

100000002 = 12810

Szukana najmniejsza liczba binarna zawierająca 8 cyfr, która składa się z 4 jedynek i 4 zer.

100001112 = 13510

Matura 2015 (maj). Zadanie 1. Problem telewidza

Matura 2015 (maj). Zadanie 1. Problem telewidza

W Problemie telewidza mamy program telewizyjny, zawierający listę filmów emitowanych w różnych stacjach telewizyjnych jednego dnia. Telewidz zamierza obejrzeć jak najwięcej filmów w całości. Jedyne ograniczenie jest takie, że telewidz może oglądać co najwyżej jeden film (stację telewizyjną) jednocześnie. Zakładamy, że jednego dnia wszystkie filmy są różne.

Program telewizyjny emisji filmów w 4 stacjach telewizyjnych:

Telewizja / stacja Film i godziny jego emisji Czas trwania emisji filmu
TV1 film 1: od 9:00 do 12:00
film 2: od 15:00 do 17:00		 3 godziny
2 godziny
TV2 film 3: od 11:00 do 16:00 5 godzin
TV3 film 4: od 12:00 do 14:00 2 godziny
TV4 film 5: od 11:30 do 12:30 1 godzina

Dla programu podanego powyżej telewidz jest w stanie obejrzeć aż trzy filmy, np.: film 1, film 4, film 2. Przyjmujemy, że telewidz nie traci w ogóle czasu na przełączanie pomiędzy stacjami (np. o godz. 12:00 z TV1 na TV3). Innymi słowy, czasy emisji filmów 1 i 4 nie kolidują ze sobą.
Rozważ następujący algorytm wyboru filmów do obejrzenia przez telewidza, w którym w kroku 2. stosuje się jedną z czterech strategii opisanych w tabeli 1.

Specyfikacja:

Dane:

T – zbiór filmów z programu telewizyjnego z godzinami emisji i czasami ich trwania,
S – strategia z tabeli 1.

Wynik:

P – zbiór filmów, które obejrzy telewidz.

Algorytm:

Krok 1. Zainicjuj P jako zbiór pusty.
Krok 2. Dopóki T zawiera jakieś filmy, wykonuj:
– stosując strategię S, wybierz ze zbioru T film x i usuń go z T
– dodaj film x do zbioru P
– usuń ze zbioru T wszystkie filmy, których czasy emisji kolidują z czasem emisji filmu x.
Krok 3. Zakończ wykonywanie algorytmu i wypisz wszystkie filmy ze zbioru P.

Tabela 1. Cztery strategie (S) w Problemie telewidza:

Strategia A Wybierz film, który trwa najdłużej, a jeśli jest takich więcej, to wybierz z nich ten, który się najwcześniej kończy. Jeśli jest więcej takich filmów,wybierz dowolny z nich.
Strategia B Wybierz film, który trwa najkrócej, a jeśli jest takich więcej, to wybierz z nich ten, który się najwcześniej kończy. Jeśli jest więcej takich filmów, wybierz dowolny z nich.
Strategia C Wybierz film, który się najwcześniej zaczyna, a jeśli jest takich więcej, to wybierz z nich ten, który się najwcześniej kończy. Jeśli jest więcej takich filmów, wybierz dowolny z nich.
Strategia D Wybierz film, który się najwcześniej kończy, a jeśli jest takich więcej, to wybierz z nich ten, który się najpóźniej zaczyna. Jeśli jest więcej takich filmów, wybierz dowolny z nich.

Przykład:
Dla podanego programu telewizyjnego zastosowanie w kroku 2. strategii A daje wynik P = {film 3}, czyli telewidz obejrzy tylko jeden film.

Zadanie 1.

Dla podanego programu telewizyjnego podaj wyniki wykonywania algorytmu po zastosowaniu strategii B, C i D:

Strategia S Zawartość zbioru P po zakończeniu wykonywania algorytmu
B P = {film 5, film 2}
C P = {film 1, film 4, film 2}
D P = {film 1, film 4, film 2}

Zadanie 2.

Zastosowana strategia S w algorytmie jest optymalna, jeśli dla każdego programu telewizyjnego wynik algorytmu (zbiór P) zawiera największą możliwą liczbę filmów, które może obejrzeć telewidz.

Uwaga:
Strategia A nie jest optymalna, ponieważ telewidz może obejrzeć trzy filmy: film 1, film 4 oraz film 2.

Dla strategii A, B i C podaj w przygotowanych tabelach przykłady programów telewizyjnych, z emisją czterech filmów w dwóch stacjach, będące dowodami, że żadna z tych strategii nie jest optymalna.

Dla każdej strategii i podanego dla niej programu telewizyjnego podaj wynik działania algorytmu oraz przykład ilustrujący, że telewidz może obejrzeć więcej filmów, jeżeli nie używa tej strategii.

Wskazówka. Podaj takie godziny emisji czterech filmów, aby telewidz był w stanie obejrzeć np. trzy lub więcej filmów, podczas gdy zastosowanie algorytmu z odpowiednią strategią daje rozwiązanie zawierające co najwyżej dwa filmy.

Dowód dla strategii A:

Telewizja / stacja Film i godziny jego emisji Czas trwania emisji filmu
TV1 film 1 (od …………………. do ………………….),
film 2 (od …………………. do ………………….)		 ………………….
………………….
TV2 film 3 (od …………………. do ………………….),
film 4 (od …………………. do ………………….)		 ………………….
………………….

Wynik działania algorytmu przy zastosowaniu strategii A:

P

Liczniejszy zbiór filmów, które może obejrzeć widz:

Z

Dowód dla strategii B:

Telewizja / stacja Film i godziny jego emisji Czas trwania emisji filmu
TV1 film 1 (od …………………. do ………………….),
film 2 (od …………………. do ………………….)		 ………………….
………………….
TV2 film 3 (od …………………. do ………………….),
film 4 (od …………………. do ………………….)		 ………………….
………………….

Wynik działania algorytmu przy zastosowaniu strategii B:

P

Liczniejszy zbiór filmów, które może obejrzeć widz:

Z

Dowód dla strategii C:

Telewizja / stacja Film i godziny jego emisji Czas trwania emisji filmu
TV1 film 1 (od …………………. do ………………….),
film 2 (od …………………. do ………………….)		 ………………….
………………….
TV2 film 3 (od …………………. do ………………….),
film 4 (od …………………. do ………………….)		 ………………….
………………….

Wynik działania algorytmu przy zastosowaniu strategii C:

P

Liczniejszy zbiór filmów, które może obejrzeć widz:

Z

 

Matura 2018. Zadanie 3. Test

Matura 2018. Zadanie 3. Test

Oceń prawdziwość podanych zdań. Zaznacz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe. W każdym zadaniu punkt uzyskasz tylko za komplet poprawnych odpowiedzi.

Zadanie 1.

Na pewnym serwerze WWW znajduje się strona napisana w języku PHP, a jej kod zawiera fragmenty w języku JavaScript. Pewien komputer-klient pobrał i wyświetlił tę stronę.
Wiadomo, że:

1. Kod PHP jest wykonywany przez komputer – serwer. P
2. Kod JavaScript jest wykonywany przez komputer – klient. P
3. Podczas wykonywania kodu PHP zawsze pobierane są dane od klienta. F
4. Podczas wykonywania kodu JavaScript mogą być pobierane dodatkowe dane zarówno od klienta, jak i od serwera. P

Wyjaśnienie:

Kod PHP jest zawsze wykonywany po stronie serwera, a do przeglądarki wysyłany jest wynik działania kodu PHP. Do działania kodu PHP nie są potrzebne żadne dane pobierane od użytkownika. Kod JavaScript jest już wykonywany po stronie przeglądarki, tak jak kod HTML. Do działania kodu JavaScript możemy pobierać dane od użytkownika z przeglądarki oraz serwera, ale nie jest to konieczne.

Zadanie 2.

1. Plakat do druku lepiej przygotować w modelu barw RGB niż CMYK. F
2. Kolor żółty jest kolorem podstawowym w modelu RGB. F
3. W wyniku nałożenia się składowych Yellow i Magenta w modelu CMYK otrzymamy kolor czerwony. P
4. W modelu barw CMYK litera C pochodzi od angielskiego słowa contrast. F

Wyjaśnienie:

RGB – jeden z modeli przestrzeni barw, opisywanej współrzędnymi RGB. Jego nazwa powstała ze złożenia pierwszych liter angielskich nazw barw:
R – red (czerwonej),
G – green (zielonej),
B – blue (niebieskiej),
z których model ten się składa. Jest to model wynikający z właściwości odbiorczych ludzkiego oka, w którym wrażenie widzenia dowolnej barwy można wywołać przez zmieszanie w ustalonych proporcjach trzech wiązek światła o barwie czerwonej, zielonej i niebieskiej.

CMYK – zestaw czterech podstawowych kolorów farb drukarskich stosowanych powszechnie w druku wielobarwnym w poligrafii i metodach pokrewnych (atramenty, tonery i inne materiały barwiące w drukarkach komputerowych, kserokopiarkach itp.). Na zestaw tych kolorów mówi się również barwy procesowe lub kolory triadowe (kolor i barwa w jęz. polskim to synonimy). CMYK to jednocześnie jedna z przestrzeni barw w pracy z grafiką komputerową.
C cyjan (ang. cyan) – odcień niebieskiego,
M magenta (ang. magenta) – w syntezie addytywnej kolor uzyskany w wyniku połączenia czerwieni i niebieskiego,
Y żółty (ang. yellow) – kolor bardzo podobny do żółtego,
K czarny (ang. black lub key colour) – kolor czarny, jednak o niezbyt głębokiej czerni.
Skrót CMYK powstał jako złożenie pierwszych liter angielskich nazw kolorów. Końcowa litera K może oznaczać albo literę ostatnią słowa black (czarny; ostatnią, ponieważ litera B jest skrótem jednego z podstawowych kolorów w analogicznym skrócie RGB) bądź skrót key colour (kolor kluczowy).

Zadanie 3.

Wskaż zdania prawdziwe dla języka SQL.

1. W wynikach zapytania postaci SELECT (…) ORDER BY (…) zawsze dostajemy rekordy uporządkowane ściśle rosnąco według wskazanego pola. F
2. Zapytanie UPDATE może zmienić wartości pól w bazie danych. P
3. Zapytanie postaci SELECT * FROM tabela1 WHERE pole LIKE (…) może w pewnych warunkach dać wszystkie rekordy z tabeli tabela1. P
4. Wynik zapytania SELECT * FROM tabela1 JOIN tabela2 ON tabela1.pole = tabela2.pole może być pusty przy niepustych tabelach tabela1 oraz tabela2. P

Wyjaśnienie:

Języku SQL jest językiem zapytań, tzn. że zadajemy pytanie za pomocą odpowiednich komend:

ORDER BY  – oznacza uporządkowanie rekordów wg wskazanego pola rosnąco ASC lub malejąco DESC.

UPDATE – za pomocą tego zapytania zmieniamy zawartość rekordów.

WHERE – służy do wyodrębniania tylko tych rekordów, które spełniają określony warunek.

JOIN – służy do łączenia wierszy z dwóch lub więcej tabel, w oparciu o powiązaną kolumnę między nimi.

Matura 2018 (maj). Zadanie 6. Centrum danych

Matura 2018 (maj). Zadanie 6. Centrum danych

Pewna firma utrzymuje centrum danych, w którym znajduje się kilkaset pracujących komputerów. Specjalny zespół pracowników odpowiada za wykrywanie i usuwanie awarii komputerów. Pliki komputery.txt, awarie.txt oraz naprawy.txt zawierają dane niezbędne do wykonania zadania.

Plik komputery.txt zawiera opisy maszyn znajdujących się w centrum w 2015 roku, każdy wiersz tego pliku zawiera kolejno:

  • numer komputera (unikatową liczbę całkowitą) – Numer_komputera,
  • sekcję, w której znajduje się komputer (sekcje oznaczone są wielkimi literami alfabetu
    angielskiego: A, B, C, …) – Sekcja.
  • pojemność dysku twardego (liczoną w gigabajtach, liczba całkowita) – Pojemnosc_dysku.

Przykład:

Numer_komputeraSekcjaPojemnosc_dysku
1R700
2N130
3E300

Plik awarie.txt zawiera informację o awariach komputerów w 2015 roku. Każdy wiersz tego pliku zawiera kolejno:

  • unikatowy numer zgłoszenia awarii – Numer_zgloszenia,
  • numer komputera, który uległ awarii – Numer_komputera,
  • datę i godzinę wystąpienia awarii z dokładnością do sekundy – Czas_awarii,
  • priorytet zgłoszenia – liczbę całkowitą określającą w skali od 1 do 10, jak krytyczna jest
    awaria – Priorytet.

Przykład:

Numer_zgloszeniaNumer_komputeraCzas_awariiPriorytet
13652015-01-01 04:40:558
22492015-01-01 06:08:243
33122015-01-01 06:33:434

W pliku naprawy.txt zapisane zostały raporty z prac, jakie wykonał zespół w 2015 roku.

Każdy wiersz tego pliku zawiera kolejno:

  • numer zgłoszenia, którego dotyczyła naprawa (mogło zdarzyć się, że jedno zgłoszenie awarii wymagało kilku napraw) – Numer_zgloszenia,
  • datę i godzinę zakończenia naprawy z dokładnością do sekundy – Czas_naprawy,
  • rodzaj naprawy (słowo restart oznacza ponowne uruchomienie komputera, wymiana –
    wymianę jednego z podzespołów komputera) – Rodzaj.

Przykład:

Numer_zgloszeniaCzas_naprawyRodzaj
22015-01-01 20:08:15restart
72015-01-02 16:30:15restart
42015-01-02 19:37:03wymiana

Dane w wierszach plików są oddzielone znakami tabulacji, pierwszy wiersz pliku jest wierszem nagłówkowym.

Za pomocą dostępnych narzędzi informatycznych podaj odpowiedzi do poniższych zadań, zapisz je w pliku wyniki.txt, a każdą z nich poprzedź numerem odpowiedniego zadania.

Pobieranie danych do programu:

Pobieranie danych z pliku tekstowego do tabeli w Access’ie wykonujemy zgodnie z poniżej przedstawionymi krokami.

Krok 1. 
Pobieramy z pliku tekstowego dane do tabeli wybierając z menu Dane zewnętrzne -> Plik tekstowy.

Krok 2.
Wskazujemy, gdzie znajduje się plik tekstowy. Te czynności powtarzamy tyle razy ile jest plików tekstowych.

Krok 3.
Ustalamy w jaki sposób są wpisane dane do pliku tekstowego.

Krok 4.
Wybieramy znak rozdzielający pola oraz zaznaczamy pierwszy wiersz zawiera nazwy pól.

Krok 5.
Wybieramy odpowiednie typy dla każdej kolumny (dla każdego pola) w tabeli. Należy pamiętać, że konieczne jest wybrania typu dla pola daty.

Krok 6. 
Wybieramy pole dla którego ma być ustawiony klucz podstawowy.

Krok 7.
Podajemy nazwę tabeli pod jaką ma być zapisana w naszej bazie.

Krok 8. 
Ustawienie relacji dla nowo utworzonych tabel w naszej bazie. Pamiętaj, że powinno się wymuszać więzy integralności.

Zadanie 1.

Znajdź 10 najczęstszych rodzajów dysków (czyli 10 najczęściej występujących pojemności) wśród komputerów w centrum. Dla każdej ze znalezionych pojemności podaj liczbę komputerów z takim dyskiem. Posortuj zestawienie nierosnąco względem liczby komputerów z dyskiem o danej pojemności.

Rozwiązanie:

Tworzymy kwerendę która będzie zawierała jedną tabelę komputery, z której wybieramy dwukrotnie pole Pojemnosc_dysku. Wykonujemy Sumy dla pola Pojemnosc_dysku, wybieramy funkcję policz, aby policzyć ile razy występuje dany rodzaj dysku. Ostatnimi elementami zakonczenia zadania jest sortowanie wystąpień dysku Malejąco, oraz ograniczenie występowań dysku do ilości 10 rekordów.

Wyniki działania kwerendy jest następujący:

Na zakończenie zapisujemy kwerendę jako Zadanie 1.

Odpowiedź:

PojemnośćLiczba
300173
20031
50031
80029
70028
60026
40020
29011
16010
22010

Zadanie 2.

Znajdź wszystkie komputery w sekcji A, w których trzeba było przynajmniej dziesięciokrotnie wymieniać podzespoły. Podaj ich numery, a także liczbę wymian podzespołów dla każdego z nich.

Rozwiązanie:

Odpowiedź:

Numer komputeraIlość wymian podzespołów
4211
12311
17112
20212

Zadanie 3.

Pewnego dnia nastąpiła awaria wszystkich komputerów w jednej z sekcji. Podaj datę awarii oraz symbol sekcji, w której nastąpiła awaria.

Rozwiązanie:

Odpowiedź:

Dniem awarii wszystkich komputerów był dzień 23-12, a było to w sekcji Q.

Zadanie 4.

Znajdź awarię, której usunięcie trwało najdłużej (czas liczymy od wystąpienia awarii do momentu zakończenia ostatniej z napraw, jakiej ta awaria wymagała). Podaj numer ogłoszenia, czas wystąpienia awarii i czas zakończenia ostatniej naprawy.

Rozwiązanie:

Odpowiedź:

Podaj numer ogłoszenia: 2087
Czas wystąpienia awarii: 2015-11-05 12:38:46
Czas zakończenia ostatniej naprawy: 2015-11-13 12:38:32

Zadanie 5.

Podaj liczbę komputerów, które nie uległy żadnej awarii o priorytecie większym lub równym 8 (wliczamy w to też komputery, które w ogóle nie uległy awarii).

Rozwiązanie:

Rozwiązanie zadania 5 w SQL:

SELECT 500-Count(*) AS Ilosc_komputerow
FROM (SELECT DISTINCT Numer_Komputera From Awarie WHERE Priorytet >= 8);

Rozwiązanie podane przez Pana Mateusza.

Odpowiedź:

Ilość komputerów: 149.

Matura 2018 (maj). Zadanie 5. Zbiornik

Matura 2018 (maj). Zadanie 5. Zbiornik

Rzeka Wirka co roku wylewała. Aby temu zapobiec, wybudowano na rzece zbiornik retencyjny. W kolejnych wierszach pliku woda.txt znajdują się dane dotyczące dziennego dopływu wody z rzeki Wirki do zbiornika retencyjnego w kolejnych dniach z lat 2008–2017. Plik zawiera 3 653 wiersze. W każdym wierszu podane są dane: data (rrrr-mm-dd) oraz liczba metrów sześciennych wody, jaka dopływała do zbiornika w ciągu doby. Dane oddzielone są znakami tabulacji.

Przykład:
2008-01-01 2275
2008-01-02 2831
2008-01-03 4615
2008-01-04 4084
2008-01-05 3258

Za pomocą dostępnych narzędzi informatycznych podaj odpowiedzi do poniższych zadań. Odpowiedzi zapisz w pliku wyniki.txt, a każdą odpowiedź poprzedź numerem odpowiedniego zadania.

Dodanie danych do programu:

Krok 1. Wybieramy opcje z pliku tekstowego.

Krok 2. Wybieramy odpowiedni plika zawierający dane.

Krok 3. 

Krok 4.

Krok 5.

Krok 6. Wskazanie miejsca gdzie ma importować dane.

Zadanie 1.

Podaj rok, w którym zbiornik retencyjny został zasilony łącznie największą liczbą metrów sześciennych wody z rzeki Wirki.

Rozwiązanie:

Rozpocząć musimy od wybrania roku z daty za pomocą funkcji =ROK(A2).

Do uzyskania odpowiedzi wykorzystamy sum częściowych.

Wybieramy sumy częściowe ze wstążki Dane.

W ustawieniach sum częściowych wybieramy Rok, Suma dla pola m3. Po wykonaniu sum mamy wynik, suma wszystkich metrów sześciennych dla każdego roku.

Do wybrania roku w którym największą liczbą metrów został zasilony zbiornik retencyjny wykorzystamy sortowanie A-Z (lub Z-A).

Odpowiedź:

Rok 2015 – 5364691 m3

Zadanie 2. 

Jaki był najdłuższy okres liczony w dniach, w którym codziennie dopływało do zbiornika retencyjnego co najmniej 10 000 metrów sześciennych wody z rzeki Wirki? Jest tylko jeden taki okres. Podaj datę początkową i datę końcową tego okresu.

Rozwiązanie:

Do obliczenia ilości dni proponuje wykonać następujące czynności. Po pierwsze sprawdzamy którego dnia powyżej 10000 m3 wody dopływa do zbiornika z rzeki. Jeżeli jest tak, należy obliczyć ile dni pod kolei spełnia ten warunek.

Po wykonaniu funkcji: =jeżeli(B2>10000;1;0) i =jeżeli(C3=1;C3+D2;0) należy sprawdzić jaki okres był najdłuższy oraz możemy sprawdzić daty od kiedy to było.

Odpowiedź:

Ilość takich dni to: 55.
Pierwsza data to: 2015-03-17.
Ostatnia data to: 2015-05-10.

Zadanie 3. 

Utwórz i podaj zestawienie łącznej liczby metrów sześciennych wody dopływającej do zbiornika retencyjnego w kolejnych miesiącach 2008 roku (od stycznia 2008 do grudnia 2008). Na podstawie zestawienia wykonaj wykres kolumnowy. Pamiętaj o czytelnym opisie wykresu (tytuł wykresu i opisy osi).

Rozwiązanie:

Przed rozpoczęciem obliczenia należy wybrać z daty nr miesiąca w 2008 roku za pomocą funkcji =MIESIĄC(A2). Następnie do uzyskania odpowiedzi wykorzystam sumy częściowe dla zaznaczonego obszaru m3 i wybrany miesiąc z daty (tylko 2008 rok).

Należy utworzyć wykres dla danych:

Odpowiedź:

m[3]Miesiąc
954331
947302
1094393
6329314
3292035
856286
1665977
1397478
2823429
17072910
22244011
17207212

Zadanie 4. 

Poniżej opisano cykl pracy zbiornika retencyjnego.

1) Na początku doby, zaraz po północy, wykonywany jest pomiar objętości wody w zbiorniku i na jego podstawie realizuje się pozostałe działania.

2) Jeśli pomiar wskazuje w zbiorniku więcej niż 1 000 000 m3 wody, to nastąpiło tzw. przepełnienie zbiornika. W takiej sytuacji, niezwłocznie po wykonaniu pomiaru i stwierdzeniu przepełnienia, nadmiar wody powyżej 1 000 000 m3 jest wypuszczany ze zbiornika.

3) Codziennie rano (o godzinie 8) ze zbiornika wypuszcza się 2% objętości wody wykazanej przez pomiar zaraz po północy. Ilość wypuszczanej wody zaokrągla się w górę do pełnych metrów sześciennych.

Uwaga: pomiar wykonany po północy 2008-02-01 wskazał 338 406 m3 wody.

Uwzględnij opisany cykl pracy zbiornika retencyjnego oraz codzienne dopływy wody z Wirki i przyjmij, że pomiar w dniu 2008-01-01 wskazywał 500 000 m3 wody, a następnie:

a) podaj dzień, w którym pierwszy raz wypuszczono nadmiar wody po przepełnieniu,

b) podaj, w ilu dniach z podanego okresu (tj. od 2008-01-01 do 2017-12-31) w zbiorniku w momencie pomiaru znajdowało się co najmniej 800 000 m3 wody,

c) podaj, ile najwięcej wody znalazłoby się w podanym okresie (tj. od 2008-01-01 do 2017-12-31) w zbiorniku (w momencie pomiaru), gdyby całkowicie zrezygnować z procedury wypuszczania nadmiaru wody powyżej 1 000 000 m3, a zbiornik miałby nieograniczoną pojemność.

Rozwiązanie:

Pkt. a)

Do wykonania punktu należy sprawdzić poprzez utworzenie tabeli z danymi takimi jak na rysunku:

Wykonałem formułę zliczającą ilość wody każdego dnia o północy poprzez policzenie w kolumnie pomocniczej ilość wody o 8 rano, ponieważ każdego dnia rano jest wylewane 2% objętości całkowitej wody.

W kolumnie ilość wody o północy znajduje się formuła:

=JEŻELI(D6+B6>1000000;1000000;D6+B6)

Musiałem wykonać funkcję jeżeli do sprawdzenia czy ilość wody w zbiorniku o północy nie przekracza 1 000 000 m3. Jeżeli przekroczyła ilość wody 1 000 000 m3 to musimy zmniejszyć ilość wody do 1 000 000 m3.

Odpowiedź zaznaczona została na czerwono, ponieważ jest pytanie: Którego dnia pierwszy raz wypuszczono nadmiar wody po przepełnieniu? Wydawać się może, że jest to dzień wcześniej, ale jest błędna odpowiedź, ponieważ tego dnia było równo 1 000 000 m3 wody w zbiorniku, zaś wylano wodę ze zbiornika 2015-04-19. W kolumnie przepełnienie zbiornika wykorzystałem funkcję:

=JEŻELI(C8>=1000000;”tak”;””)

Odpowiedź:

pkt. a)  2015-04-19

Rozwiązanie:

Pkt. b)

To zadanie należy obliczyć wykorzystując funkcję, która policzy nam ilość komórek zawierających 800 000 m3 lub więcej w danym dniu:

=LICZ.JEŻELI(C6:C3658;”>=800000″)

Odpowiedź:

pkt. b) 188

Rozwiązanie:

Pkt. c)

Punkt c w tym zadaniu wykonać należy za pomocą funkcji już wcześniej wykorzystanej licząc ilość wody w zbiorniku, tylko należy usunąć funkcję obniżająca ilość wody w zbiorniku, kiedy przekroczy 1 000 000 m3. Następnie wybrać należy największa wartość za pomocą funkcji MAX.

=MAX(G6:G3658)

Odpowiedź:

pkt. c) 1 399 242 m3

Matura 2016 (maj). Zadanie 4. Demografia

Matura 2016 (maj). Zadanie 4. Demografia

W pliku demografia.txt znajdują się informacje o urodzeniach, zgonach i ruchu naturalnym ludności w Polsce w roku 2009, w podziale na województwa i powiaty. Pierwszy wiersz w pliku jest wierszem nagłówkowym.

Fragment pliku demografia.txt:

powiat wojewodztwo ludnosc_ogolem wsp_urodzen wsp_zgonow saldo_migracji
augustowski podlaskie 58763 10,4 10,5 -1,1
bedzinski slaskie 150950 9,4 13 3,1
belchatowski lodzkie 112993 11,5 9,1 -1,6

Korzystając z dostępnych narzędzi informatycznych oraz danych zawartych w pliku demografia.txt, wykonaj podane polecenia. Odpowiedź do każdego zadania poprzedź numerem tego zadania.

Pobieranie danych do programu.

Zadanie 1.

Podaj liczbę powiatów należących do województwa mazowieckiego, w których saldo migracji było ujemne.

Rozwiązanie:

Komentarz:

Do obliczenia ilości powiatów z województwa mazowieckiego, których saldo migracji jest ujemne należy użyć filtra dla województwa – ustalamy mazowieckie, zaś dla kolumny saldo_migracji używamy filtra liczb -> mniejsza niż -> ustalamy wartość na 0 (zero). Ilość wyświetlonych wierszy jest równa 24.

Zadanie 2.

Współczynnik przyrostu naturalnego to różnica pomiędzy współczynnikiem urodzeń a współczynnikiem zgonów. Utwórz zestawienie 10 powiatów o największym współczynniku przyrostu naturalnego zawierające nazwę powiatu i współczynnik przyrostu naturalnego. Zestawienie uporządkuj alfabetycznie.

Rozwiązanie:

Komentarz:

Współczynnik przyrostu naturalnego obliczamy w nowej kolumnie G wykorzystując funkcję =D2-E2. Następnie sortujemy Z-A wg kolumny G. Następnie ukrywamy kolumny od B-F, a potem sortujemy wg powiatu tylko pierwszych dziesięć powiatów.

Zadanie 3.

Podaj nazwy czterech województw o największej liczbie ludności oraz liczbę ludności w tych województwach.

Rozwiązanie:

Komentarz:

W pierwszej kolejności należy wybrać wszystkie występujące województwa w naszym zestawieniu. Kolejnym krokiem jest obliczanie ilości mieszkańców dla każdego województwa, wykonujemy to za pomocą funkcji:

=SUMA.JEŻELI($B$2:$B$380;I2;$C$2:$C$380)

Zakres komórek z których sumujemy to wszystkie nazwy województw $B$2:$B$380, zaś suma to liczba mieszkańców w każdym powiecie należącym do województwa $C$2:$C$380. W funkcji tej występuję jeszcze I2, jest to nazwa województwa wpisana wcześniej. Sortujemy malejąco wg ilości sumy mieszkańców w danym województwie. Wybieramy pierwsze cztery rekordy.

Zadanie 4.

Współczynnik urodzeń to liczba urodzeń na 1000 mieszkańców, czyli:

Na podstawie podanej liczby ludności każdego powiatu (ludność ogółem) oraz współczynnika urodzeń w tym powiecie wykonaj dla województwa opolskiego zestawienie powiatów oraz liczby urodzeń w 2009 roku w każdym powiecie. Obliczoną liczbę urodzeń zaokrąglij w dół do najbliższej liczby całkowitej. Zestawienie posortuj alfabetycznie. Na podstawie powyższego zestawienia utwórz wykres kolumnowy ilustrujący liczbę urodzonych dzieci w poszczególnych powiatach. Pamiętaj o prawidłowym opisie wykresu.

Rozwiązanie:

Komentarz:

Rozwiązywanie zadania należy rozpocząć od wykonania sortowania wg województw, ponieważ musimy wykonać tylko dla województwa opolskiego. Następnie dla nowej kolumny tworzymy formułę odwrotną obliczającą liczbę urodzeń ze wzoru:

dzięki przekształceniu wzoru została utworzona formuła: =ZAOKR.DÓŁ(D180*C180/1000;0)

Na zakończenie tworzymy wykres z danych: nazwy powiatu województwa opolskiego i danych z kolumny G.

Plik z rozwiązaniem

Największy wspólny dzielnik

Największy wspólny dzielnik

Wyjaśnienie problemu

Największy wspólny dzielnik (NWD) dwóch liczb całkowitych – to największa liczba naturalna, która dzieli obie te liczby bez reszty.

Zatem metoda pierwsza

Największy wspólny dzielnik (NWD) znajduje się następująco. Rozkładem liczby na czynniki pierwsze, zakreślam wspólne dzielniki, mnożę zakreślone dzielniki i tak otrzymujemy liczbę będącą NWD.

Przykład

280 2 150 2
140 2 75 3
70 2 25 5
35 5 5 5
7 7 1
1

NWD(280,150) = 2 * 5 = 10

36 2 16 2
18 2 8 2
9 3 4 2
3 3 2 2
1 0 1

NWD(36,16) = 2 * 2 = 4

Zatem metoda druga

Algorytm Euklidesa jest szybkim sposobem obliczania największego wspólnego dzielnika dwóch (zwłaszcza dużych) liczb całkowitych. Polega ona na dzieleniu modulo (reszta z dzielenie).

Algorytm

Aby obliczyć NWD(a,b), wykonujemy kolejno następujące kroki:

  1. Dzielimy z resztą liczbę a przez liczbę b
    • jeżeli reszta =0, to NWD(a,b)=b
    • jeżeli reszta ?0, to przypisujemy liczbie a wartość liczby b, liczbie b wartość otrzymanej reszty, a następnie wykonujemy ponownie punkt 1.

Przykład

Liczba A = 280  B = 150

280 : 150 = 1 reszty 130
150 : 130 = 1 reszty 20
130 : 20 = 6 reszty 10
20 : 10 = 2 reszty 0

Otrzymaliśmy resztę równą zero, zatem szukany NWD będzie równy ostatniej niezerowej reszcie:

NWD(280, 150) = 10

Zatem metoda trzecia

Największy wspólny dzielnik (NWD) możemy wyznaczyć metodą Euklidesa, która polega na wyznaczeniu dwóch liczb naturalnych. Kolejnym krokiem jest sprawdzenie, która liczba jest większa i zamianie miejscami jeśli to konieczne, aby ustawić większa liczba na początku. Następnie wykonujemy odejmowanie, powstały wynik podstawiamy pod liczbę większą, gdzie powstaje nowa para. Powtarzamy te czynności do momentu, kiedy dwie liczby są równe.

Przykład

Liczba A = 280 B = 150

280 – 150 = 130
150 – 130= 20
130 – 20 = 110
110 – 20 = 90
90 – 20 = 70
70 – 20 = 50
50 -20 = 30
30 – 20 = 10
20 – 10 = 10
10 10

Ponieważ liczby są sobie równe, oznacza to, że największy wspólny dzielnik liczb 280 i 150 to 10.