Matura 2017 (maj). Zadanie 6. Wybory

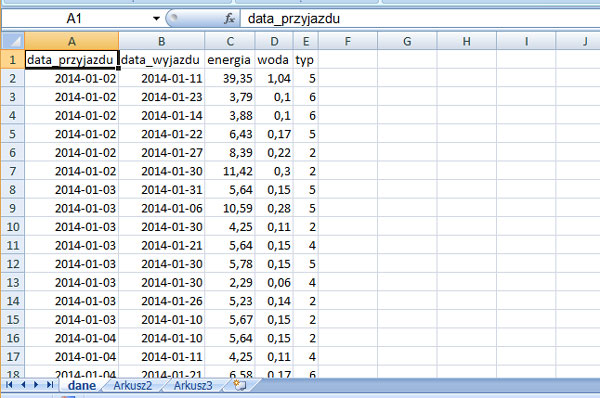
W plikach tekstowych uczniowie.txt, glosy.txt oraz kandydaci.txt zapisano wyniki głosowania w wyborach do Parlamentu Uczniowskiego pewnego liceum. Pierwszy wiersz każdego z plików jest wierszem nagłówkowym, poszczególne informacje w każdym wierszu rozdzielone są znakami tabulacji.

Plik o nazwie uczniowie.txt zawiera 2100 wierszy z informacjami dotyczącymi wszystkich uczniów szkoły. W każdym wierszu znajdują się: identyfikator ucznia (id_ucznia), imię (imie), nazwisko (nazwisko) oraz oznaczenie klasy (klasa) i rok nauki ucznia (rok_nauki).

Przykład:

id_ucznia	imie	nazwisko	klasa	rok_nauki
1600	Mateusz	Zgid	A	3
1601	Teresa	Budzisz	A	3
1602	Klaudia	Antczak	A	3

W pliku glosy.txt, w każdym z 4100 wierszy, zapisane są: identyfikator głosu (id_glosu), identyfikator głosującego ucznia (id_ucznia), identyfikator kandydata, na którego oddano ten głos (id_kandydata).

Przykład:

id_glosu	id_ucznia	id_kandydata
1	1739	67
2	1639	16
3	1746	11
4	1613	77

Uwaga: jeden uczeń mógł głosować na kilku kandydatów.

W pliku kandydaci.txt zapisano 78 wierszy z informacjami o kandydatach do Parlamentu Uczniowskiego: identyfikator kandydata (id_kandydata), imię (imie), nazwisko (nazwisko).

Przykład:

id_kandydata	imie	nazwisko
1	Faustyn	Augustowski
2	Karolina	Adamczyk
3	Milena	Karwik

Wykorzystaj dane zawarte w plikach oraz dostępne narzędzia informatyczne i wykonaj poniższe zadania. Odpowiedzi zapisz w pliku wyniki6.txt, a każdą odpowiedź poprzedź numerem odpowiedniego zadania.

Pobieranie danych do programu. Zadanie zostało rozwiązane za pomocą MS Access.

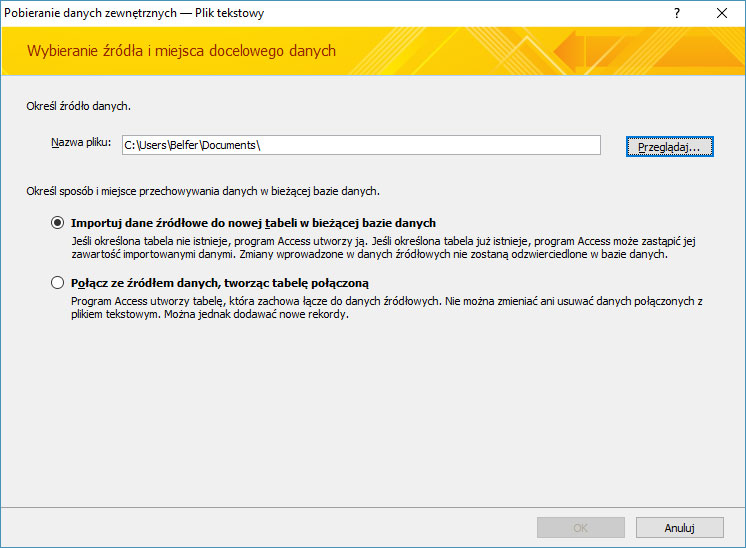
Krok 1. Pobieranie danych zapisanych w plikach tekstowych do aplikacji.

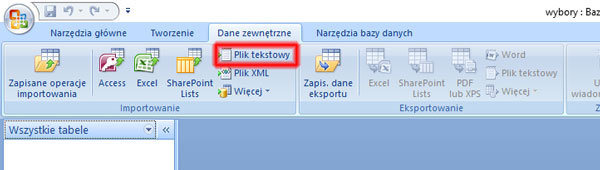
Krok 2. Wybór pliku do pobrania.

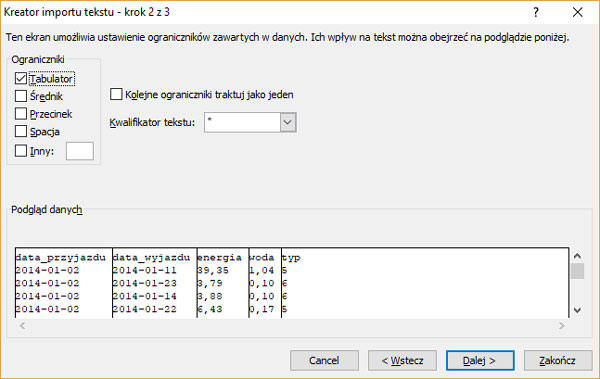
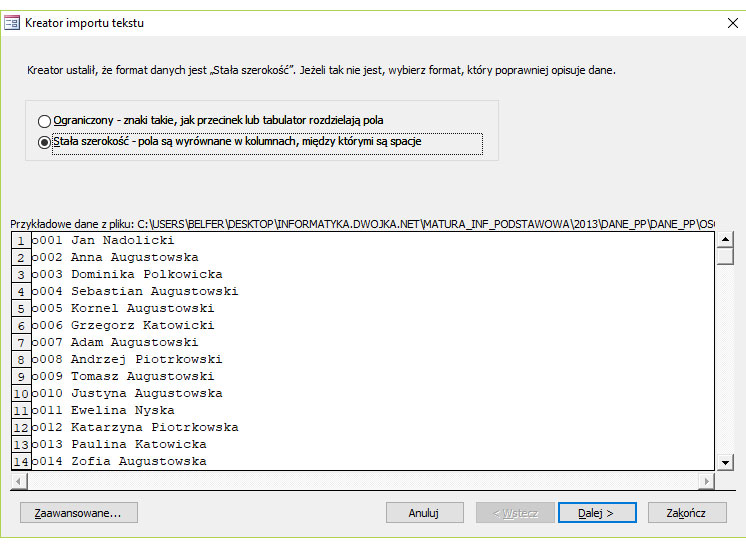
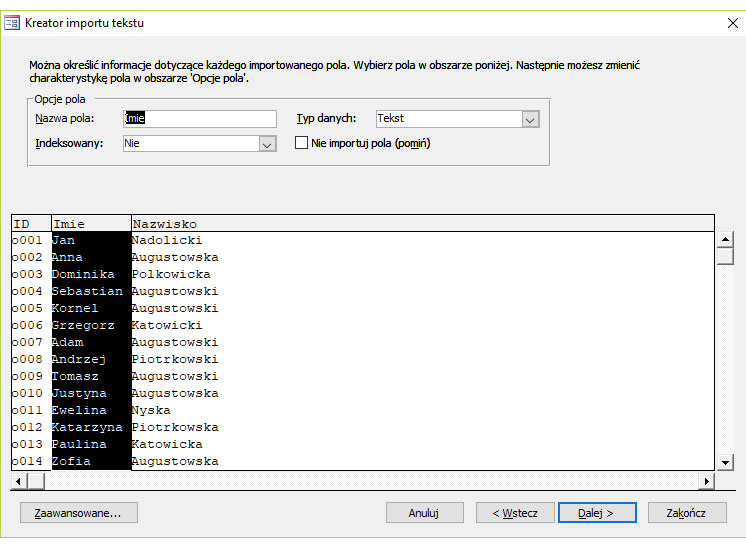
Krok 3. Kreator pobierania danych z pliku do tabeli.

Krok 4. 

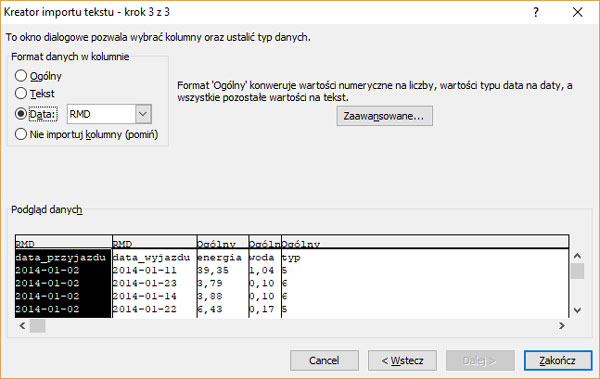
Krok 5. Sprawdzenie czy pobierane dane są odpowiedniego typu.

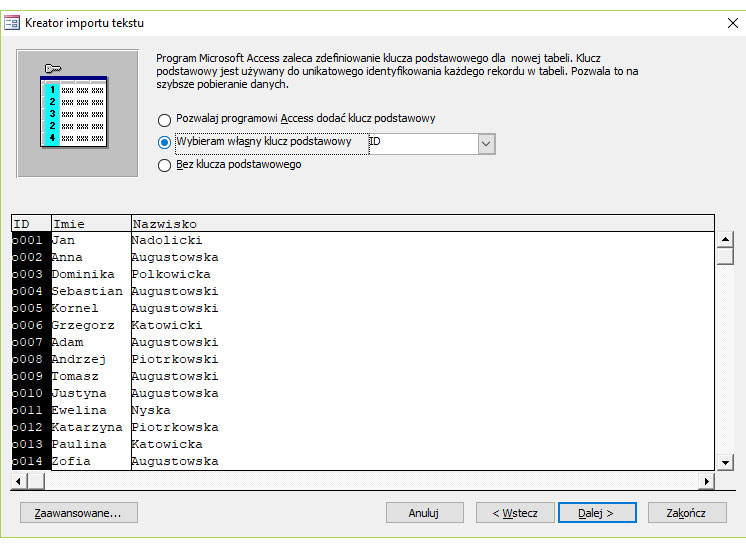
Krok 6. Wybór klucza podstawowego dla pola w tabeli.

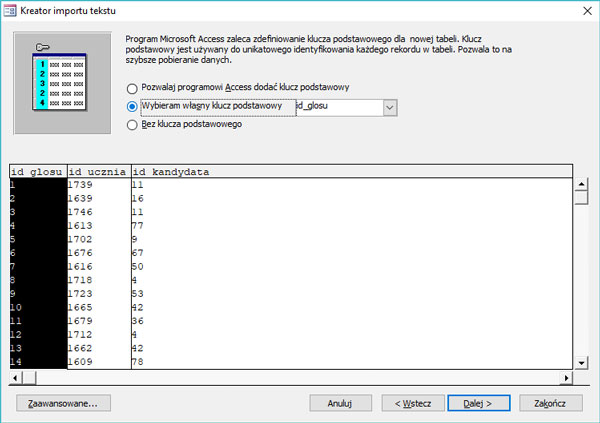
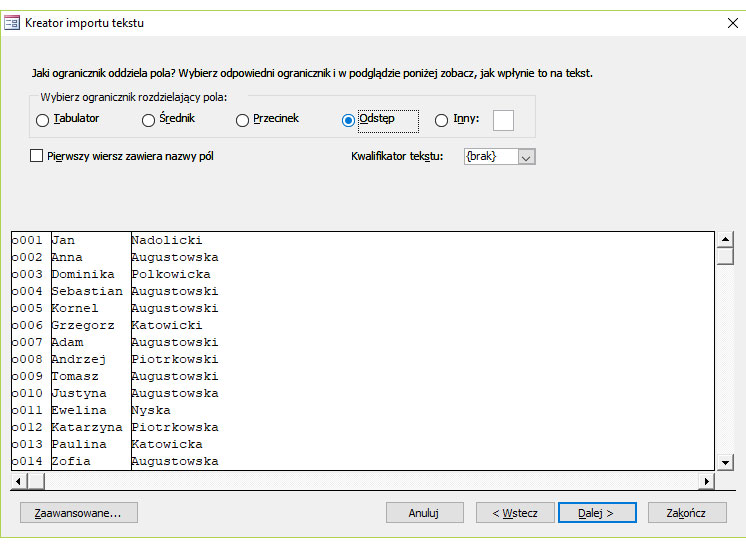
Krok 7.

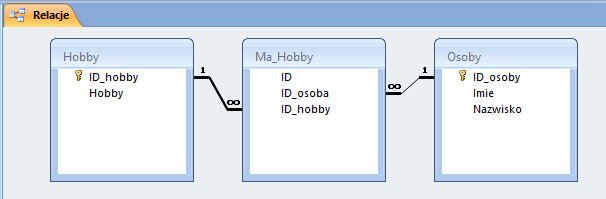
Krok 8. Tworzenie relacji.

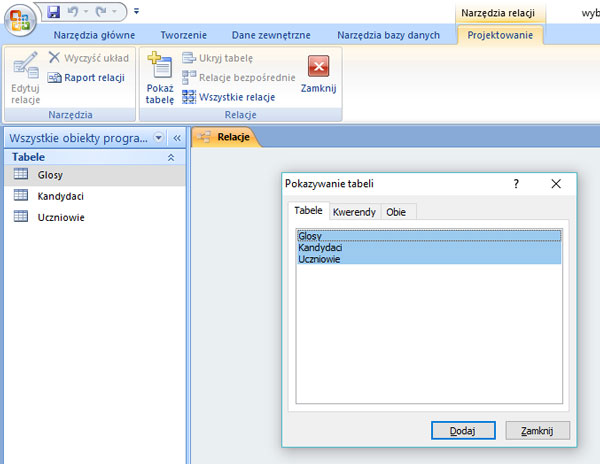
Krok 9. Należy zaznaczyć „Wymuszaj więzy integralności” przy tworzeniu relacji.

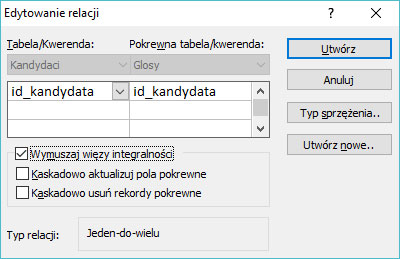
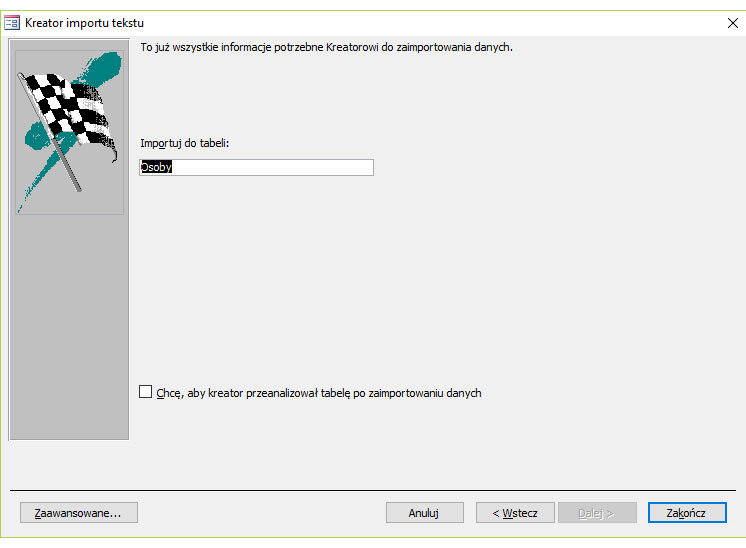
Krok 10.

Plik z danymi do pobrania.

Plik do pracy w MS Access.

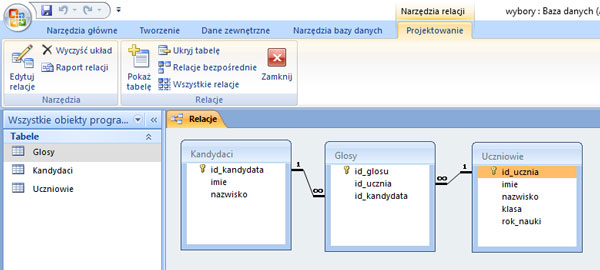
Zadanie 1.

Imiona wszystkich dziewcząt w zestawieniu kończą się literą „a”, natomiast imiona chłopców nie kończą się literą „a”. Podaj ile dziewcząt i ilu chłopców jest uczniami szkoły, w której przeprowadzono wybory.

Rozwiązanie:

Komentarz:

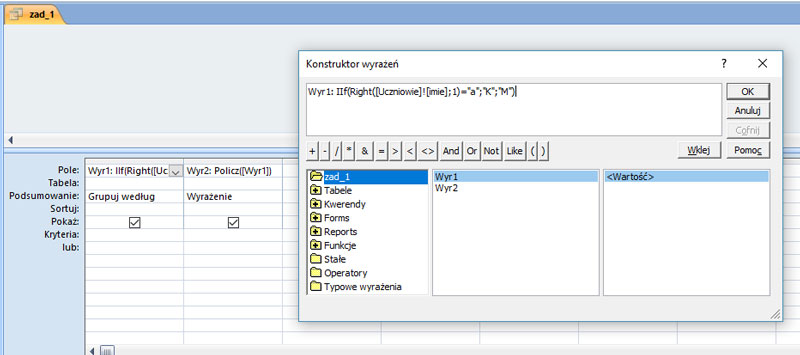
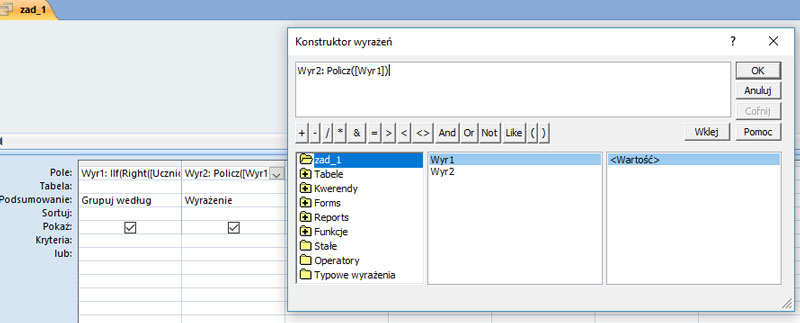
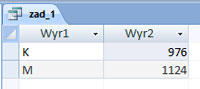
Pierwszy krokiem jest utworzenie nowej kolumny z informacją, czy podane imię jest męskie czy żeńskie. Wykonać to można za pomocą instrukcji warunkowej IIF oraz należy wybrać ostatnią literę imienia poprzez wykorzystanie funkcji RIGHT i zwrócenie ostatniej litery. Po sprawdzeniu imienia, należy policzyć ile razy występuje wyrażeniu 1 wybrana litera. Po uruchomieniu mamy wynik: K = 976, M = 1124.

Wykorzystane funkcje:
Wyr1: IIf(Right([Uczniowie]![imie];1)=”a”;”K”;”M”)
Wyr2: Policz([Wyr1])

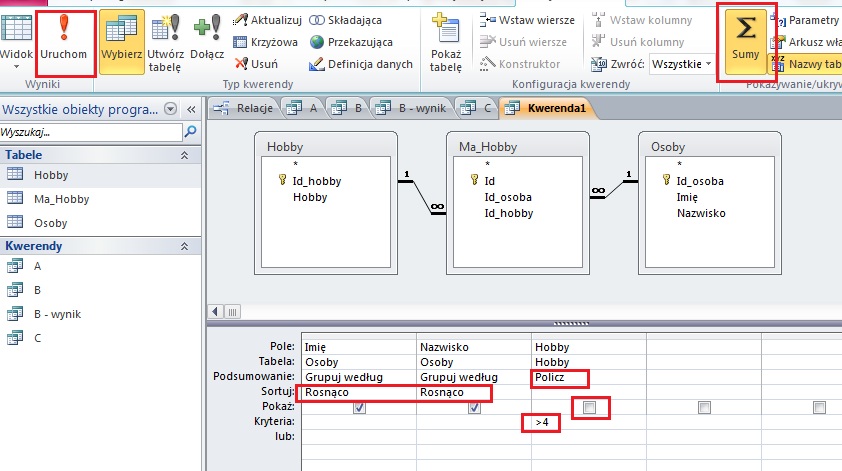
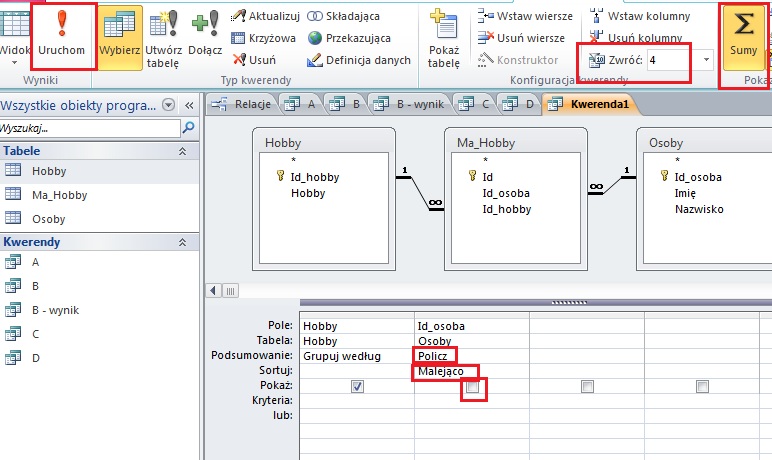
Zadanie 2.

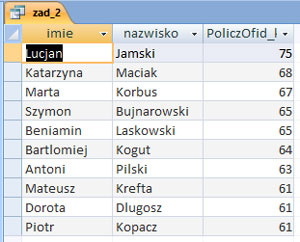
Prezydium Parlamentu Uczniowskiego (w skrócie: PPU) składa się z 10 osób, które uzyskały największą liczbę głosów. Podaj skład PPU – dla każdej osoby podaj imię, nazwisko oraz uzyskaną liczbę głosów. Zestawienie posortuj nierosnąco ze względu na liczbę uzyskanych głosów.

Rozwiązanie:

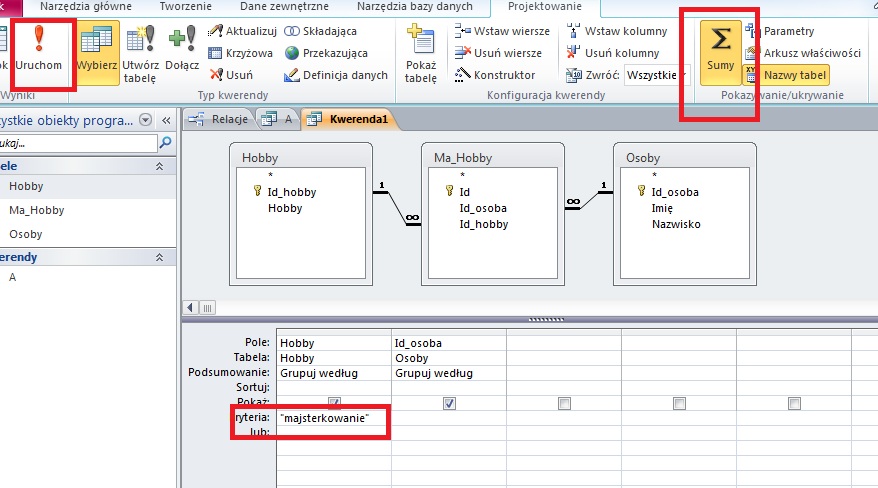
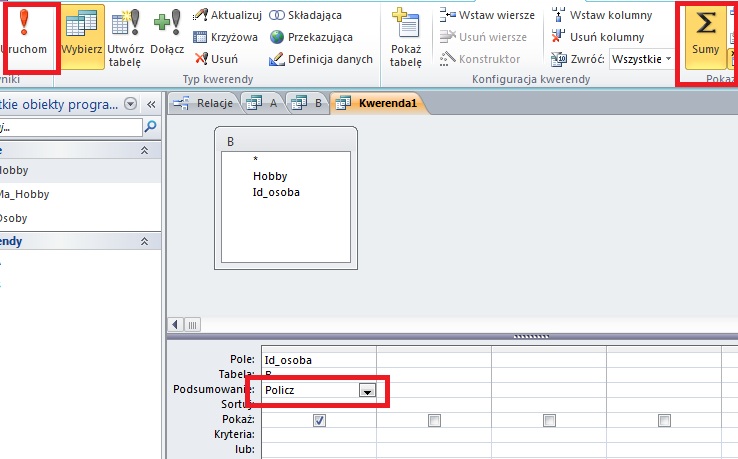
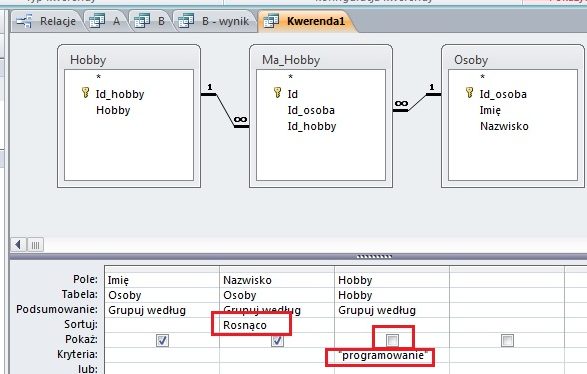
Komentarz:

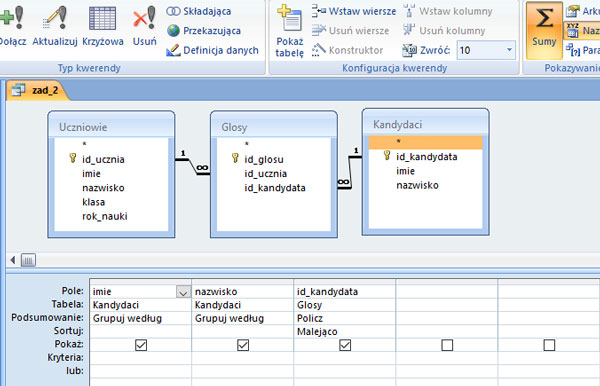
Należy utworzyć kwerendę zawierająca pola imie, nazwisko z tabeli Kandydaci orz id_kandydata z tabeli Glosy. Po wybraniu należy wybrać podsumowanie i dla pola id_kandydata należy wybrać funkcję policz. Dodatkowo należy posortować malejąca wg uzyskanych głosów (id_kandydata z tabeli Glosy). Na zakończenie należy wybrać ilość zwracanych rekordów (należy zwrócić 10).

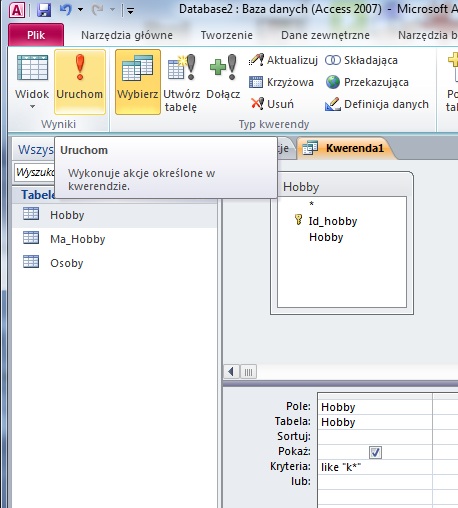
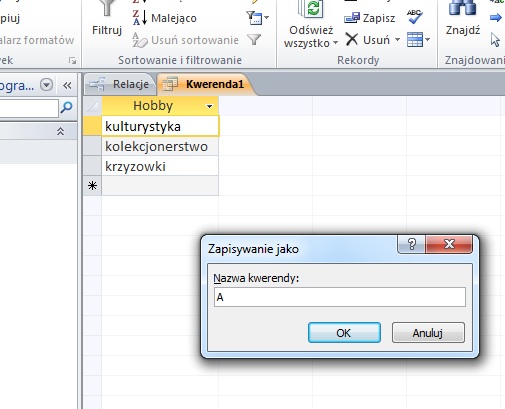
Zadanie 3.

Podaj, ilu uczniów nie wzięło udziału w wyborach (nie oddało żadnego głosu).

Rozwiązanie:

Komentarz:

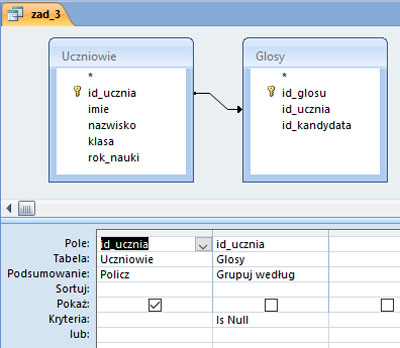
Do rozwiązania zadania należy utworzyć kwerendę wyszukującą niedopasowane dane. Tworzymy taką kwerendę dodajemy pola id_ucznia z tabeli Uczniowie oraz id_ucznia z tabeli Glosy. Należy policzyć pola id_ucznia z tabeli Uczniowie, zaś w kryteriach należy dodać kryteria IsNull dla pola id_ucznia z tabeli Glosy. Po uruchomieniu kwerendy mamy wynik: 697 uczniów nie głosowało.

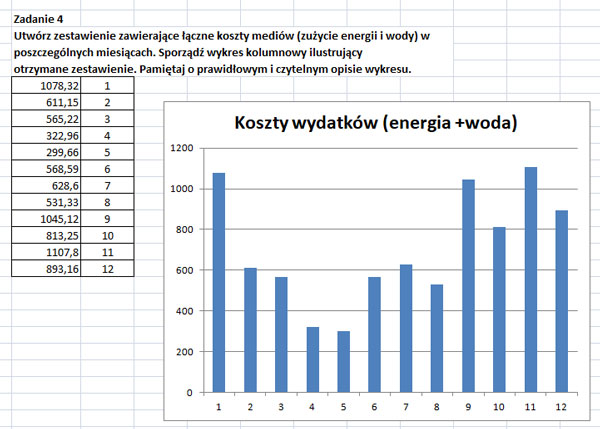
Zadanie 4.

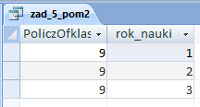
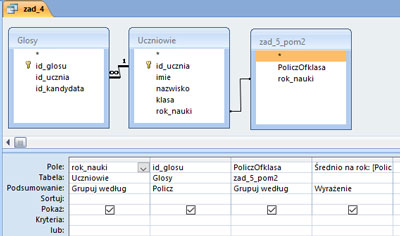
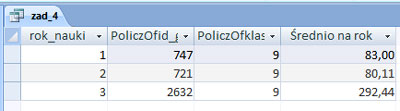
Dla każdego rocznika (rok_nauki) podaj średnią liczbę głosów oddanych przez uczniów jednej klasy tego rocznika. Wyniki podaj zaokrąglone do dwóch miejsc po przecinku.

Rozwiązanie:

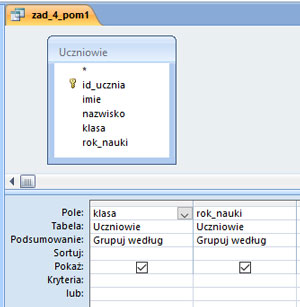
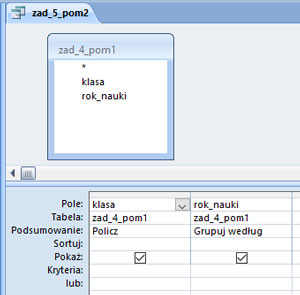
Komentarz:

Zadanie zostało wykonane poprzez utworzenie dwóch kwerend pomocniczych. Kwerendy te mają na celu wybranie ilość klas w danym roczniku. Na przykład rocznik pierwszy może zawierać inną ilość klas niż rocznik drugi. Średnia na rok jest obliczona z ilorazu ilości głosów oddanych przez uczniów w jednym roczniku na ilość klas w obliczanym roczniku.

Matura 2017 (maj). Zadanie 5. Kemping

Polskie Towarzystwo Podróżnicze prowadzi ośrodek wypoczynkowy „Cichy Kącik”. W ośrodku znajdują się domki kempingowe następujących typów: 2-, 3-, 4-, 5- i 6-osobowe. Towarzystwo rozważa zmianę sposobu naliczania opłat i w tym celu planuje analizę działalności ośrodka wypoczynkowego w roku 2014. W pliku wynajem.txt zapisana jest historia wynajmu z 2014 roku.

W każdym wierszu zapisano: datę wynajęcia domku (data_przyjazdu), datę opuszczenia domku (data_wyjazdu), koszt zużytej energii (energia), koszt zużytej wody (woda) oraz wielkość wynajętego domku (typ). Daty w pliku są podawane w formacie: RRRR-MM-DD.

Pierwszy wiersz pliku jest wierszem nagłówkowym.

Poszczególne dane w każdym wierszu rozdzielone są znakami tabulacji.

Przykład:

data_przyjazdu	data_wyjazdu	energia	woda	typ
014-01-02	2014-01-11	39,35	1,04	5
014-01-02	2014-01-23	3,79	0,10	6
014-01-02	2014-01-14	3,88	0,10	6
014-01-02	2014-01-22	6,43	0,17	5

Wykorzystaj dane zawarte w pliku wynajem.txt oraz dostępne narzędzia informatyczne i wykonaj poniższe zadania. Odpowiedzi do poszczególnych zadań zapisz w pliku tekstowym o nazwie wyniki5.txt (z wyjątkiem wykresu w zadaniu 4). Odpowiedź do każdego zadania poprzedź numerem oznaczającym to zadanie.

Dane do pobrania.

Plik z danymi utworzony w programie MS Excel 2007.

Pobranie danych do programu:

Krok 1.

Krok 2.

Krok 3.

Krok 4.

Krok 5.

Zadanie 1.

Podaj, jakiego typu domki były wynajmowane najwięcej razy.

Komentarz:

Należy policzyć każdy typ domu ile razy był wynajmowany. Występują tylko typy: 2, 3, 4, 5, 6. Wykonam to za pomocą funkcji (licz.jezeli):

=LICZ.JEŻELI($E$2:$E$1001;H3)

Rozwiązanie:

Odpowiedź:

Najczęściej wynajmowanym typem domku był typ 2, został wynajęty 204 razy.

Zadanie 2.

Dla każdego typu domków oblicz łączną liczbę dób, przez które te domki były wynajmowane.

Przykład:

data_przyjazdu	data_wyjazdu	energia	woda	typ
014-01-02	2014-01-11	39,35	1,04	5
014-01-02	2014-01-23	3,79	0,10	6
014-01-02	2014-01-14	3,88	0,10	6
014-01-02	2014-01-22	6,43	0,17	5

Domki typu 5 były wynajmowane łącznie przez 29 dób, domki typu 6 były wynajmowane łącznie przez 33 doby.

Komentarz:

Pierwsza część zadania polega na obliczeniu ile dni każdy pokój był wynajmowany. Wykonać to można na zasadzie odejmowania pamiętając, że data to liczba (odejmujemy datę młodszą od starszej).

=B2-A2

Kolejna część rozwiązania zadania polega na wykorzystaniu funkcji suma.jeżeli. Funkcja ta sumuje ilość dni każdego typu dnia.

=SUMA.JEŻELI($E$2:$E$1001;I4;$F$2:$F$1001) 

Rozwiązanie:

 

 

Zadanie 3.

Klient wynajmujący domek obowiązany jest uiszczać opłatę w wysokości czynszu oraz opłatę za zużyte media (energia elektryczna i woda). Czynsz uzależniony jest od wielkości domku oraz od czasu, na jaki wynajęto domek. Przyjęto, że:

czynsz najmu = 10 zł * liczba osób w domku (typ) * liczba dób wynajmu

Przykład:

Domek 5-osobowy był wynajęty od 1 do 10 stycznia 2014 (czyli na 9 dób). Zużyto energię elektryczną za kwotę 39,35 zł oraz wodę za 1,04 zł. Czynsz wynosi: 10 zł*5 osób*9 dób = 450 zł. Opłata za wynajem zatem wyniesie: 450 zł + 39,35 zł+1,04 zł = 490,39 zł

Utwórz zestawienie zawierające dla każdego typu domku łączną sumę opłat za wynajęcie domków tego typu. Zestawienie posortuj nierosnąco ze względu na kwotę opłat.

Komentarz:

Dodajemy kolejną kolumnę w której obliczamy opłatę za wynajem w następujący sposób (funkcja):

=E2*F2*10+C2+D2

Obliczenie sumy łącznej dla każdego typu doku wykonujemy analogicznie jak przy obliczeniu ilości dni w zadaniu 2, za pomocą funkcji:

=SUMA.JEŻELI($E$2:$E$1001;J21;$G$2:$G$1001)

W tabeli obliczamy sumę opłat za każdy typ domku, ale należy jeszcze te wartości posortować w sposób Z-A.

Rozwiązanie:

Zadanie 4.

Utwórz zestawienie zawierające łączne koszty mediów (zużycie energii i wody) w poszczególnych miesiącach. Sporządź wykres kolumnowy ilustrujący otrzymane zestawienie. Pamiętaj o prawidłowym i czytelnym opisie wykresu.

Uwaga: każdy wynajem domku przyporządkuj do miesiąca odpowiadającego dacie przyjazdu (data_przyjazdu).

Komentarz:

W pierwszej części rozwiązywania tego zadania należy dodać wartości kwot za media, tj. zużycie energii i wody w kolumnie H. To zostało wykonane za pomocą funkcji suma:

=SUMA(C2:D2)

W kolumnie I wybrałem nr miesiąca, w którym został wynajęty domek za pomocą funkcji:

=MIESIĄC(A2)

W dalszej części należy wykonać sumowanie wartości z warunkiem przypisania do poszczególnych miesięcy wynajęcia domku. Funkcja ta wygląda następująco:

=SUMA.JEŻELI($I$2:$I$1001;L31;$H$2:$H$1001)

Po wykonaniu tej czynności zostało wykonać wykres z danych znajdujących się w nowo utworzonej tabeli. Wykres w arkuszu kalkulacyjnym MS Excel wstawia się poprzez menu wstaw, wybierając wykres kolumnowy.

Rozwiązanie:

PLIK Z PRZYKŁADOWYM ROZWIĄZANYM ZADANIA.

Matura 2017 (maj). Zadanie 4. Trójki liczb

W pliku liczby.txt znajduje się 1000 trójek liczb całkowitych dodatnich rozdzielonych pojedynczymi odstępami, każda trójka – w osobnym wierszu. Liczby zapisane w pliku należą do przedziału [1, 32 767].

Plik do pobrania.

Fragment danych z pliku liczby.txt:

20634 31423 261
11009 21970 32126
26318 16336 5158
24196 14586 3545

Napisz program(y), który(e) da(dzą) odpowiedzi do poniższych zadań. Odpowiedzi zapisz
w pliku wyniki4.txt, a każdą odpowiedź poprzedź odpowiednim numerem zadania.

Zadanie 1.

Podaj, w ilu wierszach pliku z danymi liczby w trójkach są uporządkowane rosnąco.

Przykład:

Dla danych
4587 9351 28950
15010 28342 31848
30172 7492 6768
29120 21664 32328

odpowiedzią jest 2 (w dwóch wyróżnionych wierszach liczby są uporządkowane rosnąco).

Rozwiązanie:

#include <iostream>
#include <fstream>
#define N 1000
#define T 3
using namespace std;
int main()
{
 int t[T][N];
 fstream plik;
 plik.open("liczby.txt");
 if (!plik.good()) cout << "brak pliku!";
   else {
     for (int i=0; i<N;i++)
     plik >> t[0][i] >> t[1][i] >> t[2][i];
 }
 plik.close();
 // zadanie 1
 int wiersz=0;
 for (int i=0; i<N;i++)
   if ((t[0][i] < t[1][i]) && (t[1][i] < t[2][i])) {
     cout << t[0][i] << " " << t[1][i] << " " << t[2][i] << endl;
     wiersz++;
   }
 fstream wynik;
 wynik.open("wynik4.txt", ios::out);
 wynik << wiersz << endl;
 wynik.close();
 return 0;
}

Komentarz:

Pobieramy dane z pliku do zmiennych tablicowych t[0][1000], t[1][1000], t[2][1000]. Następnie sprawdzamy czy liczba t₁ jest mniejsza od t2 oraz cz liczba t₂ jest mniejsza od t₃, jeśli tak to zwiększamy wartość wiersz o jeden.

Zadanie 2.

Dla każdego wiersza wyznacz największy wspólny dzielnik (NWD) trójki liczb w nim zapisanych i podaj sumę tych dzielników.

Przykład:

Dla danych
3 6 9
34 10 4
36 20 28
16 40 56

odpowiedzią jest 17, ponieważ NWD trójek liczb w kolejnych wierszach to: 3, 2, 4, 8 (3+2+4+8=17).

Rozwiązanie:

#include <iostream>
#include <fstream>
#define N 1000
#define T 4
using namespace std;
int NWD(int a, int b) {
 while (a!=b) {
 if (a>b) a-=b;
 else b-=a;
 }
 return a;
}
int main()
{
 int t[T][N];
 fstream plik;
 plik.open("liczby.txt");

if (!plik.good()) cout << "brak pliku!";
 else {
 for (int i=0; i<N;i++)
 plik >> t[0][i] >> t[1][i] >> t[2][i];
 }
 plik.close();
 // zadanie 2
 int suma = 0;
 for (int i=0; i<N;i++) {
 t[3][i] = NWD(NWD(t[0][i],t[1][i]),t[2][i]);
 suma+=t[3][i];
 }
 fstream wynik;
 wynik.open("wynik4.txt", ios::out);
 wynik << suma << endl;
 wynik.close();
 return 0;
}

Komentarz:

Pobieramy dane z pliku do zmiennych tablicowych t[0][1000], t[1][1000], t[2][1000]. Następnie obliczamy dla każdej trójki NWD metodą Euklidesa i wynik przypisujemy do tablicy nr 4. Na koniec wykonujemy sumowanie wartości zapisanych w tablicy.

Zadanie 3.

Dla każdego wiersza oblicz sumę cyfr wszystkich liczb znajdujących się w tym wierszu.
Podaj:

• liczbę wierszy, dla których suma cyfr ze wszystkich trzech zapisanych liczb jest równa
  35;
• największą sumę cyfr w wierszu oraz liczbę wierszy, w których suma cyfr równa jest
  tej największej wartości.

Przykład:

Dla danych
45 9151 2800
2882 15040 2800 (*)
30172 2592 1102
29121 23564 320 (*)
3 243 765

W dwóch wierszach suma cyfr jest równa 35 (wytłuszczone wiersze). Maksymalną sumą jest 40, która wystąpiła 2 razy – w wierszach oznaczonych (*).

Rozwiązanie:

#include <iostream>
#include <fstream>
#define N 1000
#define T 4
using namespace std;
int sumacyfr(int c) {
 int s=0;
 while (c>0) {
 int tmp=c%10;
 c/=10;
 s+=tmp;
 }
 return s;
}
int main()
{
 int t[T][N];
 fstream plik;
 plik.open("liczby.txt");
 if (!plik.good()) cout << "brak pliku!";
 else {
 for (int i=0; i<N;i++)
 plik >> t[0][i] >> t[1][i] >> t[2][i];
 }
 plik.close();
 // zadanie 3
 int ile = 0;
 int suma = 0;
 int maksimum = 0;
 int ile_maks = 0;
 for (int i=0; i<N;i++) {
 t[3][i] = sumacyfr(t[0][i])+sumacyfr(t[1][i])+sumacyfr(t[2][i]);
 if (t[3][i] == 35)
   ile++;
   if (maksimum<t[3][i]) maksimum = t[3][i];
 }
 for (int i=0; i<N;i++)
   if (t[3][i] == maksimum)
   ile_maks++;
 fstream wynik;
 wynik.open("wynik4.txt", ios::out);
 wynik << "ilosc sumy cyfr rownych 35 : "<< ile << endl;
 wynik << "wartosc maksimalnej sumy cyfr rowna jest : "<< maksimum << endl;
 wynik << "ilosc wystepowan maksimum jest rowna : "<< ile_maks << endl;
 wynik.close();
 return 0;
}

 

Matura 2017 (maj). Zadanie 2. Liczby pierwsze

Parą liczb bliźniaczych nazwiemy dwie liczby pierwsze różniące się o 2. Liczbami bliźniaczymi są 11 i 13, gdyż obie liczby są pierwsze i różnica pomiędzy nimi wynosi 2. Para 13 i 15 nie jest parą liczb bliźniaczych, gdyż 15 jest liczbą złożoną.

Zadanie 1.

Uzupełnij poniższą tabelę. Wykonaj obliczenia i podaj odpowiedź, czy istnieje taka liczba, z którą liczba a tworzy parę liczb bliźniaczych.

Liczba a	Czy liczba a jest pierwsza?	Liczba b1=a+2	Czy liczba b1 jest pierwsza?	Liczba b2=a–2	Czy liczba b2 jest pierwsza?	Czy istnieje taka liczba b, z którą liczba a tworzy parę liczb bliźniaczych?
17	tak	19	tak	15	nie	TAK
5	tak	7	tak	3	tak	TAK
31	tak	33	nie	29	tak	TAK
41	tak	43	tak	39	nie	TAK
49	nie	51	nie	47	tak	NIE

Rozwiązanie:

Liczba pierwsza jest to taka liczba naturalna większa od 1, która posiada dokładnie dwa dzielniki: 1 i samą siebie. Sprawdzamy każdą liczby a czy jest to liczba pierwsza, jeśli nie to nawet nie musimy sprawdzać kolejnych liczb, zaś jeśli tak to sprawdzamy liczby b₁=a-2 oraz b₂=a+2. Jeśli, któraś z liczb b₁, b₂ jest liczbą pierwszą to wtedy mówimy, że liczby tworzą parę liczb bliźniaczych.

Zadanie 2.

Zapisz algorytm (w postaci listy kroków, schematu blokowego lub w wybranym języku programowania) sprawdzający, czy dana liczba należy do pary liczb bliźniaczych. Twój algorytm powinien być zgodny z poniższą specyfikacją.

Uwaga: w zapisie możesz wykorzystać tylko operacje dodawania, odejmowania, mnożenia, dzielenia, dzielenia całkowitego i brania reszty z dzielenia całkowitego, operacje logiczne oraz samodzielnie napisane funkcje.

Specyfikacja algorytmu:

Dane:

a – dodatnia liczba całkowita, a ≥ 3

Wynik:

komunikat TAK, jeżeli a należy do pary liczb bliźniaczych
komunikat NIE, jeżeli a nie należy do pary liczb bliźniaczych

Algorytm:

#include <iostream>
#include <math.h>
using namespace std;
bool czypierwsza(int a) {
  bool spr;
  if(a<2) spr = false;
  //gdy liczba jest mniejsza niz 2 to nie jest pierwsza
  for(int i=2;i<=sqrt(a);i++) {
    if(a%i==0) {
      spr = false;
      break;
    }
    spr = true;
  }
  return spr;
}
int main()
{
 cout << "Podaj liczbe: ";
 int liczba;
 cin >> liczba;
 if (( czypierwsza(liczba)&& czypierwsza(liczba-2)) || (czypierwsza(liczba) && czypierwsza(liczba+2)))
   cout << "TAK";
 else
   cout << "NIE" << endl;
 return 0;
}

Matura 2017 (maj). Zadanie 1. Szyfrowanie

Dany jest algorytm szyfrujący tekst jawny s o następującej specyfikacji:

Dane:

d – długość tekstu do zaszyfrowania, d > 1
s[1..d] – tekst jawny, ciąg znaków o długości d
k – liczba całkowita dodatnia taka, że k < d
n – liczba całkowita dodatnia taka, że n < d

Wynik:

szyfr [1..d] – zaszyfrowany tekst s

Algorytm:

od j=1 do d
 szyfr[j] ← s[j]
 i ← 1
 dopóki i ≤ d – k
 szyfr[i] ↔ szyfr[i+k]
 i ← i+n

Operacja szyfr[a] ↔ szyfr[b] oznacza zamianę w ciągu szyfr znaku z pozycji a na znak z pozycji b – i na odwrót.

Zadanie 1.

Uzupełnij tabelę – wpisz zaszyfrowany tekst, który otrzymasz w wyniku wykonania algorytmu.

s	d	k	n	szyfr
ataknadranem	12	4	2	ntdkaaeranam
maturazinformatyki	18	3	5	uatmrnziafarmotyki
stokrotka	9	1	2	tskoorkta

Rozwiązanie:

Kod w języku programowania c++:

#include <iostream>
#include <string.h>
using namespace std;
int main()
{
 char tekst[]="stokrotka";
 int d=strlen(tekst);
 cout << d << endl;
 char szyfr[d];
 int k=1, n=2;
 cout << "Tekst jawny: " << tekst << endl;
for (int j=0; j<d; j++)
 szyfr[j]=tekst[j];
int i=0;
 while(i<=d-k-1){
 swap(szyfr[i],szyfr[i+k]);
 i+=n;
 }
cout << "Tekst szyfowany: " ;
 for (int j=0; j<d; j++)
 cout << szyfr[j];
return 0;
}

Zadanie 2.

W kolumnie szyfr zapisano zaszyfrowany tekst s. Odszyfruj tekst i zapisz go w kolumnie s.

szyfr	d	k	n	s
eiindaezotinwezssyktpo	22	2	2	pieniadzetoniewszystko

Algorytm:

od j=1 do d
 szyfr[j] ← s[j]
 i ← d-n
 dopóki i > 0
 szyfr[i] ↔ szyfr[i-k]
 i ← i-n

Kod w języku programowania c++:

#include <iostream>
#include <string.h>
using namespace std;
int main()
{
 char tekst[]="eiindaezotinwezssyktpo";
 int d=strlen(tekst);
 cout << d << endl;
 char szyfr[d];
 int k=2, n=2;
 cout << "Tekst szyfowany: " << tekst << endl;
for (int j=0; j<d; j++)
 szyfr[j]=tekst[j];
int i=d-n;
 while(i>0){
 swap(szyfr[i],szyfr[i-k]);
 i-=n;
 }
cout << "Tekst jawny: " ;
 for (int j=0; j<d; j++)
 cout << szyfr[j];
return 0;
}

Zadanie 3.

Uzupełnij zapis algorytmu tak, aby w wyniku jego działania otrzymać odszyfrowany tekst s.

Uwaga: W zapisie możesz wykorzystać operacje dodawania, odejmowania, mnożenia, dzielenia, dzielenia całkowitego i brania reszty z dzielenia całkowitego, operację zamiany dwóch znaków ↔ oraz samodzielnie napisane funkcje.

Specyfikacja:

Dane:

d – długość zaszyfrowanego tekstu, d > 1
szyfr [1..d] – zaszyfrowany tekst o długości d
k – liczba całkowita dodatnia taka, że k < d
n – liczba całkowita dodatnia taka, że n < d

Wynik:

s [1..d] – tekst jawny

Algorytm:

od j=1 do d
s[j] ← szyfr[j]
i ← 1
dopóki i <= d-n-k
 i ← i+n
dopóki i >= 1
 s[i] ↔ s[i+k]
 i ← i-n

W pliku historia.txt znajdują się wartości jednostek uczestnictwa różnych funduszy inwestycyjnych w kolejnych dniach roboczych 2008 roku. W każdym wierszu znajduje się 13 danych: data oraz 12 liczb rzeczywistych (zapisanych z dwoma miejscami po przecinku), które są cenami jednostek kolejnych funduszy (A, B, C, D, E, F, G, H, I, J, K, L) w danym dniu. Wszystkie dane rozdzielone są średnikami.

Przykład:
2008-01-02;50,90;51,62;53,12;58,66;58,96;59,26;48,15;48,17;48,19;50,23;50,23;50,23
2008-01-03;50,42;51,13;52,62;57,92;58,22;58,51;48,04;48,06;48,08;50,07;50,07;50,07

Wykorzystując dane zawarte w pliku oraz dostępne narzędzia informatyczne wykonaj poniższe polecenia. Odpowiedzi zapisz w pliku zadanie6.txt, a odpowiedź do każdego podpunktu poprzedź literą oznaczającą ten podpunkt.

Rozwiązanie:
Zaczynamy od pobrania danych do arkusza kalkulacyjnego. Plik gotowy do rozwiązywania zadań jest gotowy do pobrania tu.

a) Dla każdego z funduszy podaj średnią cenę jednostki (z całego roku). Wynik zaokrąglij do dwóch miejsc po przecinku.

Do obliczenia średniej wartości ceny jednostki i zaokrąglenia do dwóch miejsc po przecinku wykonujemy za pomocą funkcji:
=ZAOKR(ŚREDNIA(B2:B252);2)

b) Podaj liczbę dni, w których ceny jednostek wszystkich funduszy były wyższe niż 33 zł. Takimi dniami były między innymi dni przedstawione w powyższym przykładzie.

 

c) Podaj cenę, która w całym roku wystąpiła najczęściej, i napisz, ile razy wystąpiła.

d) Dla każdego z dwunastu funduszy podaj najniższą i najwyższą cenę jednostki, jaką odnotowano w 2008 roku. Sporządź wykres liniowy ilustrujący otrzymane zestawienie. Pamiętaj o prawidłowym i czytelnym opisie wykresu.

Fabryka samochodów GAZELA produkuje od 2005 roku samochody osobowe czterech marek: Dama, Granta, Dorkas, Lodera. W pierwszym kwartale 2005 roku wyprodukowano 237 samochodów marki Dama, 198 – Granta, 207 – Dorkas oraz 312 – Lodera.

W każdym kolejnym kwartale, w stosunku do poprzedniego kwartału, aż do końca 2009 roku, produkcja samochodów wzrastała. Dla samochodów marki Dama – o 2%, dla samochodów marki Granta – o 2,7%, dla samochodów marki Dorkas – o 3% i dla samochodów marki Lodera – o 2%.

W wyniku kryzysu w 2010 roku wzrost produkcji został zatrzymany i przez cały 2010 rok liczba wyprodukowanych samochodów była stała – utrzymała się dla wszystkich marek na poziomie produkcji z ostatniego kwartału 2009 roku. W roku 2011 i 2012 produkcja co kwartał malała odpowiednio dla samochodu marki Dama – o 1%, samochodu marki Granta – o 1,2%, samochodu marki Dorkas – o 1,9% i samochodu marki Lodera – 2,5%.

Uwaga: Wszystkie wyliczane wartości produkcji zaokrąglaj w dół do liczb całkowitych.

Wykorzystując dostępne narzędzia informatyczne, na podstawie informacji zapisanych wyżej, wykonaj polecenia. Każdą odpowiedź, z wyjątkiem wykresu w zadaniu 4.5., zapisz w pliku wynik4.txt i poprzedź ją numerem oznaczającym zadanie.

Rozwiązanie:

Należy utworzyć skoroszyt wg szablonu na rysunku. Dane do pierwszego kwartału 2005 uzupełniamy z treści zadania, zaś kolejne kwartały obliczamy ze wzoru:

=ZAOKR.DÓŁ(B4+(B4*C9);0)

gdzie:

B4 – wartość z pierwszego (z poprzedniego) kwartału;
C9 – wartość procentowa wzrostu lub spadku produkcji samochodów;

Zadanie 4.1. (2 pkt)

Ile samochodów poszczególnych marek wyprodukowano w ostatnim kwartale 2011 roku?

Rozwiązanie:

Uzupełniamy tabelę wg lat, aż do roku 2012. Spisujemy wartości z ostatniego kwartału roku 2011. Wartości przepisujemy do pliku tekstowego.

Zadanie 4.2. (2 pkt) 

Zakładając, że spadek produkcji samochodów w następnych latach będzie wyglądał tak samo jak w roku 2011 i 2012, wskaż markę samochodu, którego kwartalna produkcja najwcześniej będzie mniejsza od produkcji tej marki z pierwszego kwartału 2005 roku. Podaj markę samochodu, liczbę wyprodukowanych samochodów oraz kwartał i rok, kiedy to nastąpi.

Rozwiązanie:

Do rozwiązania zastosowałem formatowanie warunkowe zmieniające kolor komórek z warunkiem mniejsze niż wartość komórki w pierwszym kwartale 2005 roku.

Zadanie 4.3. (2 pkt)

Podaj – dla każdej marki – w ilu kwartałach, w okresie od początku 2005 roku do końca 2012 roku, produkcja przekraczała 300 sztuk?

Rozwiązanie:

Należy utworzyć tabelę pomocniczą zawierająca nazwy modeli samochodów oraz dla każdej utworzyć formułę:

=LICZ.JEŻELI(B4:AG4;”>300″)

Zakres komórek jest podawany od początku roku 2005 do końca roku 2012. Powtórz tę instrukcję dla wszystkich aut.

Zadanie 4.4. (1 pkt)

Podaj, ile samochodów łącznie wyprodukowano w fabryce GAZELA do końca 2010 roku.

Rozwiązanie:

To zadanie jest bardzo nietypowe, należy wykorzystać funkcję

=SUMA(zakres)

Wynik działania funkcji na rysunku.

Zadanie 4.5. (3 pkt)

Utwórz wykres kolumnowy 3D prezentujący wielkość produkcji każdej marki samochodu w kolejnych latach od roku 2005 do roku 2012. Zadbaj o czytelność wykresu.

Rozwiązanie:

Utwórz nową tabelę z kolumnami sumującymi produkcję każdego auta w każdym kolejnym roku wg tabelki poniżej.

 

Baltazar spisuje informacje o swoich znajomych i ich hobby, które przechowuje w plikach. W każdym pliku informacje zapisane w wierszach są rozdzielone pojedynczymi znakami odstępu.

Plik Osoby.txt zawiera 200 wierszy z informacjami o znajomych: Id_osoba, Imię, Nazwisko.
Przykład:
o001 Jan Nadolicki
o002 Anna Augustowska

Plik Hobby.txt zawiera 50 wierszy z informacjami o rodzajach hobby: Id_hobby, Hobby.
Przykład:
h001 numizmatyka
h002 historia

Plik Ma_Hobby.txt przechowuje w 400 wierszach informacje o tym, czym interesują się znajomi Baltazara: Id, Id_osoba, Id_hobby.
Przykład:
1 o152 h005
2 o065 h043

Wykorzystując dane zawarte w tych plikach oraz dostępne narzędzia informatyczne, wykonaj poniższe polecenia. Odpowiedzi zapisz w pliku zadanie5.txt, a odpowiedź do każdego podpunktu poprzedź literą oznaczającą ten podpunkt.

Narzędziem jakim się posłużymy będzie MS Access. W pierwszym kroku musimy pobrać dane z plików tekstowych do programu. Wykonujemy to realizując poniższe kroki:

Krok 1:
Pobieramy dane z pliku tekstowego wybierając Dane zewnętrzne → Plik tekstowy.

Krok 2:
Przechodzimy kreator Pobieranie danych zewnętrznych. Przykładowe pobieranie danych znajduje się poniżej.

Krok 3:
Tworzymy relację wg rysunku poniżej. Tak przygotowaną bazę możemy używać do rozwiązania zadań, do pobrania tu.

1. Podaj wszystkie rodzaje hobby rozpoczynające się od litery „k”.

Rozwiązanie:
Wybieramy wstążkę tworzenie → projekt kwerendy. Wybieramy tabelę hobby i dodajemy do nowej kwerendy. Następnie dodajemy pole hobby z tabeli Hobby do kwerendy. Kryteria jakie musimy dodać to jest wpisanie like „k*” i ostatnim krokiem jest uruchom kwerendę.
Zapisujemy kwerendę jako A.
Wynik kwerendy należy skopiować do pliku tekstowego jako rozwiązanie.

2. Podaj, ile osób interesuje się majsterkowaniem.

Rozwiązanie:
Wybieramy wstążkę tworzenie → projekt kwerendy. Wybieramy tabelę hobby, Ma_Hobby, Osoby, które mamy dodać do kwerendy. Z wybranych tabel dodajemy pola: Hobby z tabeli Hobby oraz Id_osoba z tabeli Osoby.
Zapisujemy kwerendę pod nazwą B. Wyniku działania kwerendy mam 7 rekordów, ale jeśli chcielibyśmy teraz policzyć nasze rekordy to jest ich 8, ponieważ jeden rekord się powtarza.
Tworzymy kwerendę B – wynik, aby policzyć ile jest rekordów wyświetlanych w kwerendzie B. Robimy to wybierając ikonę Sumy. Dodajemy pole ID_osoby z kwerendy B do nowej kwerendy i podsumowanie wybieramy Policz i dajemy uruchom. Na koniec zapisujemy zmiany w kwerendzie.

3. Utwórz zestawienie imion i nazwisk tych osób, których zainteresowaniem jest programowanie. Zestawienie posortuj niemalejąco, alfabetycznie według nazwisk.

Rozwiązanie:
Wybieramy wstążkę tworzenie → projekt kwerendy. Do kwerendy dodajemy table: hobby, Ma_Hobby, Osoby. Z tabel dodajemy pola: Imię i nazwisko z tabli Osoby i Hobby z tabeli Hobby. W polu nazwisko ustawiamy sortuj na rosnąco. Odznaczamy Pole hobby, aby nie wyświetlało się w wynikach, zaś do tego pola dodajemy kryterium „programowanie”. Uruchamiamy kwerendę. Zapisujemy kwerendę, jako C.

4. Utwórz zestawienie imion i nazwisk tych osób, które mają więcej niż 4 rodzaje hobby. Zestawienie posortuj niemalejąco, alfabetycznie według nazwisk, a tam, gdzie nazwiska się powtarzają – według imion.

Rozwiązanie:
Wybieramy wstążkę tworzenie → projekt kwerendy. Wybieramy pola imię i nazwisko z tabeli Osoby i pole Hobby z tabeli Hobby. Ustawiamy sortowanie Nazwisk i imion na rosnąco, Włączamy sumę, w hobby podsumowanie ustawiamy na policz, odznaczamy pokaż i kryteria ustawiamy na większe od 4. Zapisujemy kwerendę, jako D.

5. Podaj wszystkie rodzaje hobby, którymi interesuje się największa liczba osób.

Rozwiązanie:
Wybieramy wstążkę tworzenie → projekt kwerendy. Wybieramy tabele: hobby, Ma_Hobby, Osoby. Dodajemy pola na Hobby oraz Id_osoba z tabeli Osoby. Odznaczamy pokaż dla pola Id_osoba oraz dodajemy Sortowanie ustawiając na malejąco. Włączamy Sumę, w podsumowaniu dajemy policz dla pola Id_osoba. Wartość zwróć ustawiamy na 5 i dajemy uruchom. Kwerendę zapisujemy, jako podpunkt E.

Uwaga:
Wszystkie wyniki kwerend zapisz w pliku tekstowym zadanie5.txt.

 

Gotowe rozwiązanie 

 

 

Matura 2012 (maj). Zadanie 2. Diamenty

W sejfie jubilera znajduje się n diamentów wycenionych odpowiednio na d₁, …, d_n złotych, przy czym żadne dwa diamenty nie są w tej samej cenie. Jubiler nie ujawnia cen diamentów, co oznacza, że tylko on zna ceny d₁, …, d_n.
Dla zainteresowanych klientów jubiler wykonuje operację porównania cen diamentów: dla wskazanych numerów i oraz j podaje, czy diament o numerze i ma wyższą cenę, niż diament o numerze j.
Przyjmijmy następujący sposób oznaczania wyniku operacji porównania cen:
większe( i , j ) = prawda, gdy d₁ > d
większe( i , j ) = fałsz, gdy d₁ < d

1. Poniżej prezentujemy pewien algorytm korzystający z operacji porównania cen:

 Krok 1. j ← 0
 Krok 2. i ← 1
 Krok 3. dopóki i < n
   jeżeli większe(i, i i + 1) to j ← j + 1
   i ← i + 1
 Krok 4. wypisz j

Uzupełnij poniższą tabelę, podając wyniki działania powyższego algorytmu po jego wykonaniu dla wskazanych danych.

n	d1, …, dn	Wynik algorytmu
4	5 2 1 6	2
4	2 5 1 2	1
4	1 2 3 4	0
4	4 3 2 1	3

Komentarz:
Musimy podać wartość zmiennej j. Zmienna j jest zwiększona o jeden pod warunkiem, że funkcja większe(i,j) zwróci prawdą (true). Prawda jest wtedy, kiedy element i tablicy jest większy od elementów i+1, czyli element sprawdzany jest większe od elementu następnego.

Algorytm

#include <iostream>
#define N 4
using namespace std;
int d[N] = {1,2,3,4};
bool wieksze(int i, int j) {
  if (d[i]>d[j]) return true;
  else return false;
}
int main()
{
  int j=0;
  int i=0;
  while (i<N-1) {
    if (wieksze(i,i+1)) j++;
    i++;
  }
  cout << j << endl;
  return 0;
}

 

2. Zapisz algorytm (w postaci listy kroków, schematu blokowego lub w wybranym języku programowania), który dla podanego ciągu cen diamentów znajduje numer diamentu o najwyższej cenie. W algorytmie zastosuj operację większe porównania cen dwóch diamentów.

Specyfikacja:

Dane:

n – liczba naturalna większa od zera oznaczająca liczbę diamentów
d₁, …, d_n – ceny diamentów o kolejnych numerach 1, 2, …, n; ceny dwóch różnych diamentów są różne

Wynik:

i – numer diamentu o najwyższej cenie

Algorytm:

#include <iostream>
#define N 4
using namespace std;
int d[N] = {2,5,1,2};
bool wieksze(int i, int maks) {
  if (d[i]>d[maks]) return true;
  else return false;
}
int main()
{
  int maks=0;
  int i=0;
  while (i<N-1) {
  if (wieksze(i,maks)) maks = i;
  i++;
 }
  cout << maks << endl;
  return 0;
}